Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Kocurek & Tangier’s Prescribed Wake Model
Kocurek & Tangier (1976) have derived a prescribed wake model similar to that of Landgrebe using the same set of generalized equations for the tip vortex trajectories, but with different coefficients based on another series of subscale rotor experiments. This model attempts to include the number of blades as well as the blade lift distribution (through the twist rate) in the modeling of the axial settling rates. The generalized equation for k is
*, = в + C (JzQ, (10.65)
where В — —0.0007296>tw and C = — 2.3O2O60tw. The other coefficients are: m = 1.0 — 0.25е°’О4О&м and n = 0.5 — O. O1720tw. The equation for k2 is
k2 = -(CT ~ CTo)1/2, where CTo = bn(-B/C)l/m. (Ю.66)
The radial contraction rate parameter X is given by X = 4.0*/Ct, with A = 0.78, as in Landgrebe’s model. No inner vortex sheet is used in the Kocurek & Tangier model.
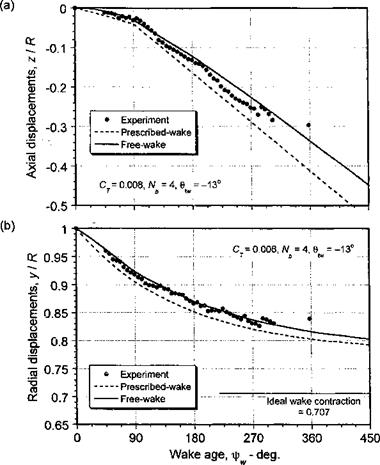
An example showing the expected quality of the predicted wake geometry and hover performance that can be made using a prescribed wake model is shown in Figs. 10.31 and 10.32. It is found that in this case the prescribed wake tends to slightly overpredict both the axial displacements and the radial contraction of the tip vortices. Results from a FVM are
|
Figure 10.31 Comparison of prescribed and free-vortex wake methods with experimental measurements of the tip vortex locations in hover, (a) Axial displacements, (b) Radial displacements. Four-bladed rotor; Ct = 0.008. |
also shown in Fig. 10.31 and 10.32. Notice that the FVM gives slightly better predictions of both the wake geometry and the hovering performance of the rotor albeit at a greater computational expense.
