Linear Source Distribution

Consider a linear source distribution along the x axis (xl<x <x2) with a source strength of o(x) = ct0 + a,(x — xx), as shown in Fig. 10.10. Based on the principle of superposition, this can be divided into a constant-strength element and a linearly varying strength element with the strength o(x) = axx. Therefore, for the general case (as shown in the left-hand side of Fig. 10.10) the results of this section must be added to the results of the constant-strength source element.

The influence of the simplified linear distribution source element, where o(x) = o1x, at a point P is obtained by integrating the influences of the point elements between xl-*x2 (see Fig. 10.11).

FIGURE 10.11

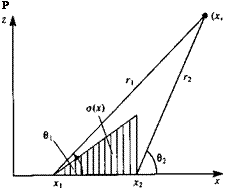Nomenclature for calculating the influence of linearly varying strength source.

Details of the integration are presented in Appendix В (Eq. (B.13)), and the results are

(10.47)

where rlt r2, 0i, and 02 are defined by Eqs. (10.15) and (10.16). The velocity components are obtained by differentiating the velocity potential (Appendix B, Eqs. (B.14) and (B.15))

m = ^ [Jln p + (*! – x2) + z(02 – 0X)

S [2 ln?,+:^-ад]

CTi Г* ~ Ф 4яІ 2

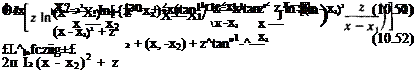Substitution of rk, вк from Eqs. (10.15) and (10.16) results in

When the point P lies on the element (z = 0±, xi<x<x2), then Eq.

(10.50) reduces to

Ф = j1 [(*2 – *x) In (x – де,) – (x2 – xl) In [x – x2 – x(x2 – *1)] (10.53)

At the center of the element this reduces to

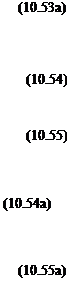-£<*М-г¥!-г)

Also, on the element

° Г, x – xi , Л, СГ,

W = ± — JC 2

and at the center of the element

CTi t

and

w = ±-(x2-xl)