Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Linearized Theory
Smelt and Davies [4] developed a semiempirical theory for the effect of a propeller on a wing for lightly loaded propellers, where w « V. Although linearized, the method is of value in many STOL ^applications
and is based on interpolating between two limiting cases by empirical means.
First, consider the case in which the chord of the wing c is small in comparison with the slipstream diameter D1. If the lift is increased on the wing submerged in the slipstream, we would expect the circulation to increase for this portion of the wing. Hence at the edge of the slipstream additional trailing vorticity would be generated. However, for c « D1 the additional induced effects due to the vortices would be negligible. Thus the lift of the wing in the slipstream would simply be increased in proportion to the square of the slipstream velocity or
AL = ipcDtCMV + h’j)2 – V2]
 |
or
In (8-19) vi’j is the velocity induced at the wing by the propeller, which is assumed to be lightly loaded so that (nq/F)2 ^ 0.
Now consider the other extreme in which c » Dt. For this case a very small trailing vortex at the slipstream boundary would give rise to a large downwash at the wing in the slipstream and would produce a decrease in the angle of attack, hence a decrease in the circulation. Thus for this limiting case the changing circulation produces effects tending to oppose the change so that the circulation is constant across the wing.
Г = icC, V = jcClt(V + Wl),
where Ch is the C, for the submerged portion of the wing. Thus the increment in lift AL is
AL = jpDjcC
Hence the change in wing CL is
ЛС
L 4 s у
In a comparison of (8-20) with (8-19), Ref. 4 states ACL in general as
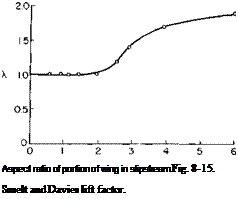
A CL = Ct^f^A. (8-21)
The factor X must lie between 1 and 2 and in general is a function of the aspect ratio of the portion of the wing in the slipstream. This function obtained empirically by Smelt and Davies is presented in Fig. 8-15. In
calculating the aspect ratio for propellers in proximity to a fuselage the submerged area should include that buried in the fuselage.
For the case in which the circulation is constant (A = 1.0) the induced velocities will remain unchanged. The changes in the induced drag coefficient can thus be readily calculated. Using a sub = 1 for the wing with slipstream,
w
C,
= CDiVF + Wl/
 |
Because CD. (V + и1,)2 = CD. V2, it follows that there is no change in the induced drag due to the slipstream. This could have been deduced directly
from the fact that the circulation remains unchanged. Hence the kinetic energy of the trailing vortex sheet per unit length, which has already been shown to equal the induced drag, is unchanged.
For the case in which A # 1, Г changes and the induced drag does not remain constant. However, because CD. is inversely proportional to the aspect ratio, and this case represents an infinite aspect ratio, it seems reasonable to assume that the induced drag remains unchanged.
