Non-planar wake

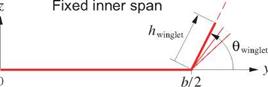
Another interesting case is a non-planar wake, such as that produced by a wing with winglets, which were originally developed by Whitcomb [49]. A winglet acts much like a span extension in that both spread out the shed vorticity, which reduces the velocities and kinetic energy in the Trefftz plane, and thus reduce Di. A span increase does this more effectively than a winglet, but on the other hand a winglet produces a smaller increase in the root bending moment.

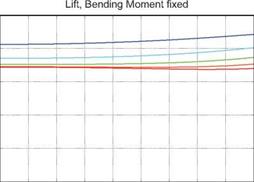
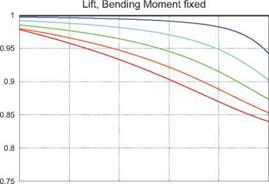
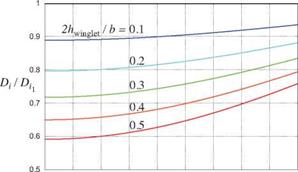
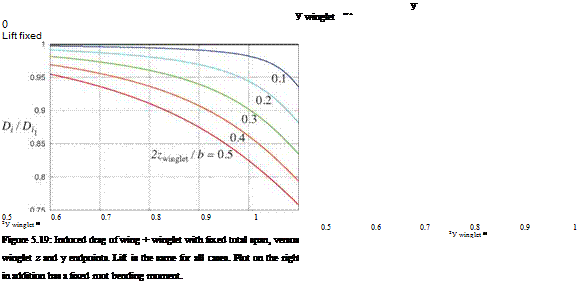
Figures 5.18 and 5.19 show two possible ways to parameterize the geometry of the wing+winglet combi­nation, and the resulting Di relative to the no-winglet case value Dil. Results both without and with the root bending moment constraint are shown. The bending moment constraint is seen to put a floor on the

Di/Di-і ratio at about 0.84, which is comparable to the minimum value of the best flat-wing case shown in Figures 5.16 and 5.17. The only apparent advantage of the winglet is that much of this benefit can be obtained with a smaller overall span. The conclusion is that winglets are effective mainly in cases where the overall span is limited by other than structural constraints. The relative merits of winglets and various other types of non-planar lifting surface systems is discussed by Kroo [47].

Lift fixed
0 10 20 30 40 50 60 70 80 90 ^ winglet і de9 ] Figure 5.18: Induced drag of wing + winglet with fixed inner span, versus winglet height and angle above horizontal. Lift is the same for all cases. Plot on right in addition has a fixed root bending moment. The no-winglet case with elliptical loading provides the reference value Dil, and also the fixed lift and bending moment values.
0 10 20 30 40 50 60 70 80 90 ^winglet і de9 ]
z	Fixed total span
z winglet