NUMERICAL EXAMPLE

The jet transport of Sec. 9.1 is used for the example, in horizontal flight at sea level. The data needed for the calculation is as follows:

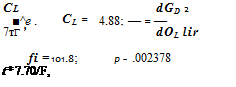CDe = .016 +

WS = 60 psf;

Ve = [2(WIS)lpCLj^;

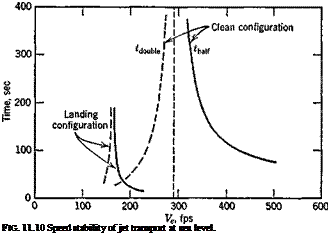With this data, the values of CL and Ve at (L/D)max are, respectively, C’L = .595 and V — 290 fps. The result of the calculation with (11.5,5) is shown in Fig. 11.10. There is positive “speed stability” above 290 fps, but the characteristic time to half is large, in excess of 75 sec. In the low – speed range (sometimes referred to as “the backside of the polar,” with reference to the CL — CD “polar” diagram), the motion is unstable, with time to double falling as low as 30.5 sec at 0L = 1.6. A low-speed landing approach with this speed characteristic is undesirable from a handling – qualities standpoint (see Sec. 12.8). On the other hand, the example corre­sponds to cruising flight, not landing, since wheels and flaps are retracted.

The speed stability is in fact quite sensitive to the drag characteristics of the airplane. Thus, suppose that undercarriage and flaps have been lowered on the jet transport, with large increases in parasite and included drag reflected in the polar equation

1 20 2

0D = 0.20 + (11.5,6)

Irr

The results for this case, also shown on Fig. 11.10, are very different. The divergence time to double is now greater than 30 sec for all speeds above about 99 mph.