Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Prediction of the far field pressure spectrum: a novel approach
In a recent paper Morino, Leotardi & Camussi (2010) proposed a novel approach for estimating the far field pressure Power Spectrum (PSD) by the knowledge of the PSD of the pressure on the boundary surface, provided that the region where the flow is rotational and/or nonlinear is adequately thin. In order to accomplish this, the PSD of the pressure at any given point (either in the field or on the boundary) is evaluated in terms of the Power Spectral Density (PSD) of the transpiration velocity over the boundary surface. This contribution is denoted as given by equivalent sources xb.
The approach briefly described therein is based upon a formulation that falls within the general class of potential-vorticity decompositions for the velocity field of the type
v = V<f + w, (6)
where w is any particular solution of the equation
Vxw = Z. (7)
with Z := Vx v denoting the vorticity field.
The decomposition given in Eq. 6 is valid for any vector field and Eq. 7 is a necessary and sufficient condition for the validity of Eq. 6. Here, we assume w to be defined so as to have
w = 0 (8)
outside of the vortical region, , which is defined as the region where the vorticity Z is not negligible.
For incompressible flows, the continuity equation reads
V – v = 0 (9)
Combining with v = V<p + w, one obtains
V2^ = a, where a = —V – w (10)
 |
 |
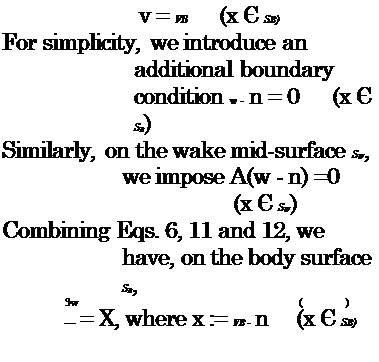In order to complete the problem, the boundary conditions have to be considered. For viscous flows, the boundary condition over SB is the no-slip condition:
The numerical formulation of the above equations can be determined both in the physical and in the Fourier domain but it is not reported here for
the sake of brevity. We just point out that, after discretization using piecewise constant approximation and Fourier transform, the following linear relationship can be achieved:
Pf = HpB. (21)
the symbol t denotes the Fourier transform of the discretized counterpart of the pressure and the equation represents the desired relationship between the field pressure (subscript F) and the boundary pressure (subscript B).
By using classical Wiener-Khintchine relationships, the above equation can be expressed in terms of the PSD matrix Sv. Thus, using Eq. 21, we have
SPF = H* SPB HT (22)
which is the desired relationship between the PSD matrix SPF of the pressure at NV arbitrary points in the region K3W and the PSD matrix SPB of the pressure at NB points on SB.
The expression in Eq. 22 allows one to evaluate the field-pressure PSD from the boundary-pressure PSD, thereby providing a link between two sets of experimental data (PSD of field pressure and PSD of surface pressure), often considered independent.
