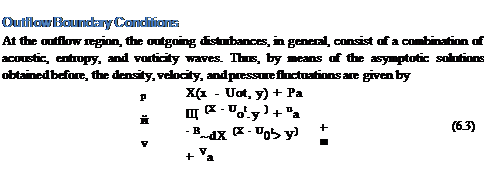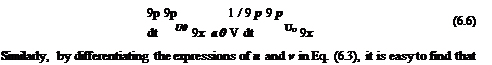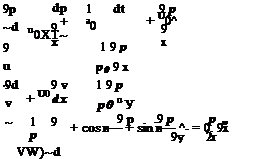At boundaries where there are only outgoing acoustic waves, the solution is given by an asymptotic solution (5.25) as follows:
where V(e) = a0[M cos в + (1 – M2 sin2 в)1/2]. The subscript ‘a’ in (pa, ua, va, pa) in Eq. (6.1) indicates that the disturbances are associated with the acoustic waves alone. By taking the time t and r derivatives of formula (6.1), it is straightforward to find that for arbitrary function F the acoustic disturbances satisfy the following equations:
P
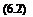
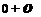 / 1 д д й
/ 1 д д й
V (в) дt дГ 2r/ V
p
Eq. (6.2) provides a set of radiation boundary conditions.

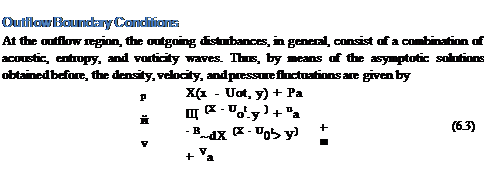
|
where the explicit form of (pa, ua, va, pa) may be found in Eq. (6.1). The functions X, f, and F are entirely arbitrary. It is observed that the total pressure fluctuation comes only from the acoustic component of the outgoing disturbances. Thus, the appropriate outflow boundary condition for p is the same as that of Eq. (6.2). On writing out Cartesian coordinates in two dimensions, it is
|
|
|
d p.9 p p
+ cos в — + sin в — + ^~ d x dy 2r
|
|
|
|
|
|
|
where в is the angular coordinate of the boundary point.
By differentiating the expression for p in Eq. (6.3) with respect to t and x, the following equation is found:
|
|
|
dp dp dp dp„
— + U0—— = — + u0—. 91 0 dx 91 0 dx
|
|
|
|
|
But pa = pa/a2 = p/a0 andp is known from Eq. (6.4). By eliminating pa, the outflow boundary condition for p becomes
|
|
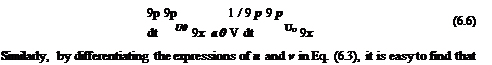 |
 |
|
du 9 u 1 9 p 91 0 dx p0 dx
9 v 9 v 1 9 p
dt ^ U° 9x p0 9y ’
In summary, the outflow boundary conditions are as follows:
|
|
|
|
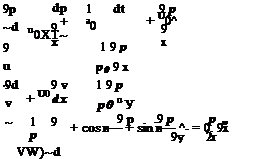 |
|
|

![]()
![]() / 1 д д й
/ 1 д д й![]()