Simple Vortex
A simple or free vortex is a flow field in which the fluid elements simply translate along concentric circles, without spinning about their own axes. That is, the fluid elements have only translatory motion in a free vortex. In addition to moving along concentric circular paths, if the fluid elements spin about their own axes, the flow field is termed forced vortex.
A simple or free vortex can be established by selecting the stream function, ф, of the source to be the potential function ф of the vortex. Thus, for a simple vortex:
It can be easily shown from Equation (2.42) that the stream function for a simple vortex is:
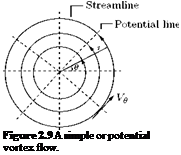
It follows from Equations (2.42) and (2.43) that the velocity components of the simple vortex, shown in Figure 2.9, are:
Vg = Vr = 0. (2.44)
2 nr
Here again the origin is a singular point, where the tangential velocity Vg tends to infinity, as seen from Equation (2.44). The flow in a simple or free vortex resembles part of the common whirlpool found while paddling a boat or while emptying water from a bathtub. An approximate profile of a whirlpool is as shown in Figure 2.10. For the whirlpool, shown in Figure 2.10, the circulation along any path about the origin is given by:
Г = ф V ■ dl
/* 2n
Vgrdg.
 |
0
z
Since there are no other singularities for the whirlpool, shown in Figure 2.10, this must be the circulation for all paths about the origin. Consequently, q in the case of vortex is the measure of circulation about the origin and is also referred to as the strength of the vortex.











