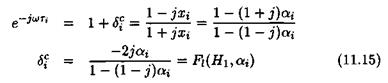THE DETAILED METHOD

• The difficulty of the method of subsection 1.3 is that uncertain scalars Xi are to be handled, which vary between —oo and Too. If methods ex­ist for deciding whether v0S{M{ju>)) is less than a given strictly positive value at a fixed frequency w (see e. g. the previous subsection), it is not so obvious to decide whether v0S(M{juj)) is zero, especially when bounds of Ms ( M j w ) ) are computed instead of the exact value.

On the other hand, it would be more convenient to represent the fre­quency response e-^T> with a real non repeated scalar. As a first reason, the computational methods of the previous subsection are difficult to ex­tend to the case of real repeated scalars. As a second and more import­ant reason, the gap between the bounds tends to increase with repeated scalars. Nevertheless, this requirement imposes to split the circle corres­ponding to e~^T into two half circles (see Figure 11.2): the bottom half circle (between 1 and -1) and the top half circle (between -1 and 1).

• In this context, the uncertain scalar Xi is rewritten as:

so that aj Є [0, 1] corresponds to Xi X [0, X oo)? i. e. to the bottom half circle. As a consequence:

with:

As in subsection 1.3, the model perturbation Д2 = diag{5{,…, 6CN) can be rewritten as an LFT F^W., Д2), where:

Д2 = diag(ai,… ,aN) (11.17)

Here again, the initial interconnection structure M – Д of Figure 11.4.a is transformed into the new equivalent interconnection structure M — Д of Figure 11.4.b, where M = M and Д = diag(A, Д2).

An upper bound of u°£{M{ju))) is now to be computed. If this upper bound is strictly greater than 1, a lower bound of the robust delay mar­gin can be deduced. An upper bound of this margin can also be obtained with a lower bound of u^(M(ju)).

• If the upper bound ofv^(M(jco)) is less than 1 at the previous step, no destabilizing value of the delays can be found on the bottom half circle. The delay frequency response is thus rewritten as:

1 , p _ Іхі ~ 1 = -1 + (1 + j)aj

1 jXi + l 1 + (j – l)«f —2(1 — qj)

1 – «і 4- jcti

with:

The top half circle (between -1 and 1) is obtained when сц є [0, 1]. As above, a new interconnection structure M — A is computed, in which the model perturbation Д contains the original mixed model perturbation Ді and the real non repeated scalars aj’s.

An upper bound of u^(M(ju)) is calculated. If it is less than 1, an infinite robust delay margin is obtained. Otherwise, a lower bound of this margin is deduced. In this case, an upper bound of the margin can also be obtained with a lower bound of

Remark: the interest of the above method is that it is geometrically very simple. See nevertheless (Scorletti, 1997) for a more complex, but potentially richer method.