THE KINETIC ENERGY T

The kinetic energy of the moving masses (elevator, levers, pistons, rods, etc.) can for small displacements always be expressed in the form

т = ¥ейе2 + ^КЬ + ¥Л2 (H-3,1)

The coefficients of this equation are generalized inertias, and could be com­puted by integrating the energy associated with de and Oj over all the moving material system. These inertias are assumed to be constants.

THE GENERALIZED FORCE &n

The generalized force is given by (5.12,8), where W is the work done by the external aerodynamic and inertia forces during a virtual displacement of the system. Let it be expressed as

AW = He A<5e + P AsP + J ksj + ATT, (11.3,2)

where sP and Sj are the displacements of the forces P and J respectively,

and Wt is the work done by the inertia forces. Thus

The kinematic derivatives dsPjdbe, etc., are simple constants, readily deter­mined from the geometry of the linkage.

We now require the derivatives of W{. The inertia force field is given by

= —(a — Ї’) dm (11.3,4)

where a is acceleration of dm relative to Fj given by (5.1,8) and r’ = [x, y, zT is its position vector in FB. The work done in a virtual displacement by this field is

A Wi =J (dfx. Аж + dfy. Д у + dfz. A z) (11.3,5)

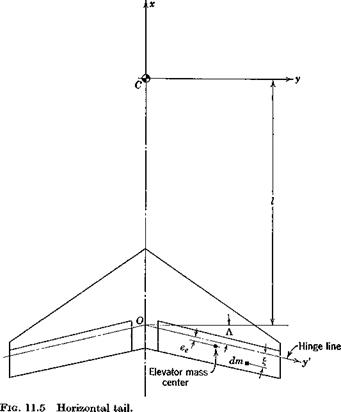
where the integration is taken over the whole control system. To carry out this integration exactly clearly requires complete information about the masses, sizes, and locations of all the moving elements. It is in principle a straightforward albeit tedious process. In the interests of simplicity we neglect all contributions to W{ except those of the elevator surface itself, and that we treat as a lamina lying in the xy plane. The relevant geometry is shown in Fig. 11.5. The displacement of the element dm is in the direction Cz and of magnitude f ASe. Hence only the last term of (11.3,5) is nonzero, so that

А1Г, =jdf::£Ade

On using (11.3,4) and (5.1,8), remembering that z — x = у = 0, we get

vanishes. The first is, by virtue of the definition of mass center,

jgdm = meee (11.3,8)

where me is the mass of both elevators, and ee is as shown in Fig. 11.5. The second integral is the product of inertia of the elevator w. r.t. its hinge line and the у axis. It is denoted

jx£dm = Pex (11.3,9)

Equations (11.3,7) now read

dWt

dOj

and finally, on combining (11.3,10) and (11.3,3) we get the generalized forces = — = He + hip + ki2J – Wo, – Pex(Pr – Я.) (11-3,11)

0Oe

dW

^» = ГТ———– 1" k21P + k22^

dVj

where [ky] is the matrix of kinematical gearings dsPjdde, etc.