The momentum integral equation

The accurate evaluation of most of the quantities defined above in Sections 7.3.2 and 7.3.3 requires the numerical solution of the differential equations of motion. This will be discussed in Section 7.11. Here an integral form of the equations of motion is derived that allows practical solutions to be found fairly readily for certain engineer­ing problems.

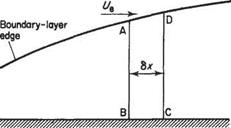
The required momentum integral equation is derived by considering mass and momentum balances on a thin slice of boundary layer of length 6x. This slice is illustrated in Fig. 7.21. Remember that in general, quantities vary with x, i. e. along the surface; so it follows from elementary differential calculus that the value of a quantity / say, on CD (where the distance from the origin is. v + 6x) is related to its value on AB (where the distance from the origin is x) in the following way:

f(x + 6x) ~f{x) + (7-54)

First the conservation of mass for an elemental slice of boundary layer will be considered, see Fig. 7.21b. Since the density is assumed to be constant the mass flow balance for slice ABCD states, in words, that

Volumetric flow rate into the slice across AB = Volumetric flow rate out across CD

+ Volumetric flow rate out across AD + Volumetric flow rate out across BC

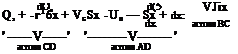The last item in the volumetric flow balance allows for the possibility of flow due to suction passing through a porous wall. In the usual case of an impermeable wall Vs — 0. Expressed mathematically this equation becomes

Note that Eqn (7.54) has been used, Q,- replacing/where

Qi =

Cancelling common factors, rearranging Eqn (7.55) and taking the limit 6x —> d. v leads to an expression for the perpendicular velocity component at the edge of the boundary layer, i. e.

The definition of displacement thickness, Eqn (7.16), is now introduced to give

-ft**

/=8

pftx

(v/V

Ч8*

(c)

y – Momentum balance

(d) Forces in ^-direction (e) Momentum fluxes in x – direction

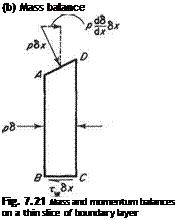
The у-momentum balance for the slice ABCD of boundary layer is now consid­ered. This is illustrated in Fig. 7.21c. In this case, noting that the у-component of momentum can be carried by the flow across side AD only and that the only force in the у direction is pressure,* the momentum theorem states that the

The force of gravity is usually ignored in aerodynamics.

Rate at which ^-component The net pressure force in the у direction of momentum crosses AD = acting on the slice ABCD

Or in mathematical terms

pV*6x = (/>w – pi)6x

Thus cancelling the common factor 6x leads to

Pv-Pi =pVl

It can readily be shown from this result that the net pressure difference across the boundary layer is negligible, i. e. pw ~ pi, as it should be according to boundary-layer theory. For simplicity the case of the boundary layer along an impermeable flat plate when Ue = C/oc(=const.) and Vs = 0 is considered, so that from Eqn (7.56)

d<5* , /d<5*2

Ve _ U°° dJ ^ Pw “Pl ~ pU°° Vd^J

It must be remembered, however, that the boundary layer is very thin compared with the length of the plate thus dS*/dx – c 1, so that its square is negligibly small. This argument can be readily extended to the more general case where Ue varies along the edge of the boundary layer. Thus it can be demonstrated that the assumption of a thin boundary layer implies that the pressure does not vary appreciably across the boundary layer. This is one of the major features of boundary-layer theory (see Section 7.3.1). It also implies that within the boundary layer the pressure p is a function of x only.

Finally, the x-momentum balance for the slice ABCD is considered. This case is more complex since there are both pressure and surface friction forces to be con­sidered, and furthermore the x component of momentum may be carried across AB, CD and AD. The forces involved are depicted in Fig. 7.21d while the momentum fluxes are shown in Fig. 7.21e. In this case, the momentum theorem states that

Rate at which / Rate at which / Net pressure force

momentum leaves ] — I momentum enters I = I in x direction acting across CD and AD/ V across AB / on ABCD

p8 -(p8 + -^(p8)6x j Ту,6х "————————- ‘ ‘ ‘—– *—- ‘ on BC on CD on AD

rS = pu*dy. Jo

out across CD

(7.57)

on AB

where

Mi,

After cancelling common factors, taking the limit 8x —► dx and simplification Eqn (7.57) becomes

dp _ TT dUe

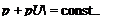dx P e dx

After substituting Eqn (7.56) for Ve, introducing the definition, Eqn (7.17), of momentum thickness and using the result given above, Eqn (7.58) reduces to

This is the momentum integral equation first derived by von Karman. Since no assumption is made at this stage about the relationship between rw and the velocity gradient at the wall, the momentum integral equation applies equally well to laminar or turbulent flow.

When suitable forms are chosen for the velocity profile the momentum integral equation can be solved to provide the variations of 6, 8*, в and Cf along the surface. A suitable approximate form for the velocity profile in the laminar boundary layer is derived in Section 7.6.1. In order to solve Eqn (7.59) in the turbulent case additional semi-empirical relationships must be introduced. In the simple case of the flat plate the solution to Eqn (7.59) can be found in closed form, as shown in Section 7.7. In the general case with a non-zero pressure gradient it is necessary to resort to computa­tional methods to solve Eqn (7.59). Such methods are discussed in Section 7.11.