THE SERVO EQUATION

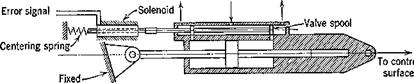
The pair of equations (11.3,13) do not normally give the whole picture. The control system illustrated in 11.4 is intended to operate with 6j as near to zero as possible. Typically a hydraulic system for this application would sense 6j as an error, and control the flow of high-pressure fluid to the piston so as to reduce it. A solenoid-controlled servo that could perform this function is illustrated in Fig. 11.6. The ports are such that the actuator is forced to follow the valve spool. In this case the error signal might be generated by a displacement transducer attached to the link A В of Fig 11.4 and used via an intervening electronic system to position the value spool. Alternatively, an entirely mechanical linkage could connect the valve spool to the pilot’s control. Servos like this one have the characteristic that the volume rate of flow of oil is very nearly proportional to the valve error, regardless of load.

High-pressure Oil return supply Oil return Fig. 11.6 Schematic of solenoid-controlled hydraulic servo.

Since the flow rate is proportional to the velocity of point A, which is a linear combination of Se and 6j, and since the valve error is proportional to 0 j, the servo equation in this case would be

ade + 6j = bOj (11.3,16)

Adding this equation to (11.3,13) completes the system, and has the effect of transferring J to the autonomous set of state variables, leaving only P as a nonautonomous input. The functioning of the servo itself in the neighbor­hood of an equilibrium point, as an uncoupled system, is described by putting Д F, a, and q = 0, leading to the control system equations (in Laplace trans­forms)

as

From this equation the ДSJP transfer function can readily be found. The characteristic equation is found by expanding the determinant of the 3×3 matrix, and is a cubic.

If the servo is powerful enough that в j may be assumed to be identically zero, then a substantial simplification results. In that case (11.3,16) is super­fluous and J can be eliminated via (11.3,12), i. e.

j = {I eJ be-hxP) (11.3,18)

&22

If furthermore the inertial coupling IeJ is negligibly small, which can be ensured by design, we get the desirable simple result

J = — —P = kP (11.3,19)

^ 22

Assuming both the above conditions to hold, the first system equation reduces

and gives a second-order transfer function connecting P and Д<5е. The corre­sponding equation with the a and q terms present is obtained from (11.3,13a) as

-HrAv + [(meeeFe – Hp. s – #J Да – {Pexs + meeeVe + Ha)q

+ (V – Hyt- Hs) Ade = KP (11.3,21)

where

Although perfect dynamic balance of the elevator surface may not always be achieved, the inertia coupling terms are often small. If they can be neglected, we get the simplest equation that still contains the essential ingredients of the control dynamics—i. e. the inertia of the control elements and the aerodynamic feedbacks:

-Hr AY – (HAs + Ha) Да – Hgq + (IjP – Hhs – Ht) ASe = KP (a)

(11.3,22)

With similar assumptions, the equations for the other two control systems are Rudder system:

For the aileron system, dx is the downward deflection of the right-hand surface, assumed equal to the upward deflection of the left-hand surface. Ia is the generalized inertia of the entire system comprising both surfaces and all connected parts, but H is the aerodynamic hinge moment on one surface only.