Two-dimensional Source and Sink

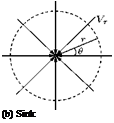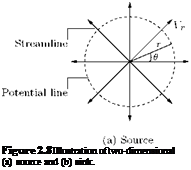
Source is a potential flow field in which flow emanating from a point spreads radially outwards, as shown in Figure 2.8(a). Sink is potential flow field in which flow gushes towards a point from all radial directions, as illustrated in Figure 2.8(b).

Consider a source at origin, shown in Figure 2.8(a). The volume flow rate q crossing a circular surface of radius r and unit depth is given by:

q = 2nrVr, (2.38)

where Vr is the radial component of velocity. The volume flow rate q is referred to as the strength of the source. For a source, the radial lines are streamlines. Therefore, the potential lines must be concentric circles, represented by:

ф = A ln(r), (2.39)

where A is a constant. The radial velocity component Vr = дф/dr = A/r.

Substituting this into Equation (2.39), we get:

2nrA

—— = q

r

or

A = ±.

2n

Thus, the velocity potential for a two-dimensional source of strength q becomes:

In a similar manner as above, the stream function for a source of strength q can be obtained as:

where в is the orientation (inclination) of the streamline from the x-direction, measured in the counter­clockwise direction, as shown in Figure 2.8(a). Similarly, for a sink, which is a type of Bow in which the fluid from infinity flows radially towards the origin, we can show that the potential and stream functions are given by:

where q is the strength of the sink. Note that the volume flow rate is termed the strength of source and sink. Also, for both source and sink the origin is a singular point.