Vorticity Diffusion Effects and Vortex Core Growth

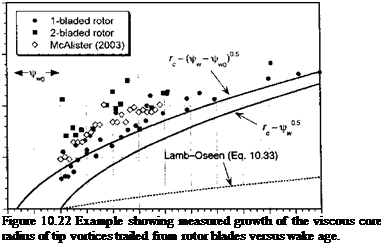
The vortex core dimension is an important parameter that can be used to help define the structure and evolution of tip vortices. Half of the distance between the two velocity peaks shown in Fig. 10.18 can be considered as the average (nominal) viscous core radius. This region is where most (but not all) of the vorticity in the tip vortex is concentrated. This core quantity is plotted as a fraction of blade chord, c, in Fig. 10.22 as a function of wake age, Jrw. It is apparent that there is a fairly rapid but asymptotic-like growth in the core. The blade passage event at i/’b = — 2зт/Nb temporarily alters the growth trend, and a

slight decrease in core size is usually observed. This is fundamentally a vortex stretching problem. This stretching effect is more evident for a two-bladed rotor (or for a rotor with higher number of blades) because the tip vortex does not have time to convect very far through the flow and is subsequently much closer to the following blade. After the blade passage, the viscous core continues to grow with a similar rate. The difficulties in measuring the vortex properities at older wake ages is compounded by the tendency for the flow to become aperiodic (see Section 10.5.1).

0.2

о

3 0.15

тз со

£

о 0.1

га с о со

<5 0.05 Е Ъ с о

2 0

-180 0 180 360 540 720 900

Wake аде, – deg.

A simple quantitative model of the growth in vortex core radius with time can be based on Lamb’s result for laminar flows – see Lamb (1932), Chigier & Corsiglia (1971), and Ogawa (1993). This result shows that without external velocity gradients (which can cause stretching and so will affect the core development) the core radius varies with the square root of age according to rc(t) — *j4avt. Starting from the Lamb-Oseen swirl velocity profile model in Eq. 10.9 then a change of variable to x — r(4vt)~l//2 gives the swirl velocity in the vortex according to

Vr0(x) = ‘;—- —f=[1 – exp(-x2)]. (10.31)

2nx^/4vt

Now, by definition, the core radius, rc corresponds to the value of r when Vq reaches a maximum, so differentiating the latter equation with respect to x gives

11 , 9 ‘ —9 3 9 exp(-xz) – f 2exp(-x )

у/. yZ

= db^[(l+2xI)ex*-x2)~l]’ (1032)

which must be zero for a maximum. This gives the solution x = 1.1209, and so the core radius grows according to the relation

rc(t) = 1.1209/4vt = *j4avt, (10.33)

where a = 1.25643. See also Question 10.6.

In practice, because of turbulence generation, the actual diffusion of vorticity contained in the vortex is known to be much quicker than using Eq. 10.33 (i. e., with molecular diffusion only being allowed by this model). It can be expected that the tip vortex initially exhibits a predominantly laminar behavior; thereafter the vortex progressively becomes turbulent. The tendency toward turbulence generation must be related to the vortex Reynolds number, Rev = Tt)/v, among other factors such as rotational stratification effects, which are discussed later in Section 10.6.5. The rate of development of the turbulent structures near the core will alter the effective diffusion rate of vorticity from within the vortex.

These effects, albeit very complicated on a fundamental level, can be incorporated into a model core growth equation using an average “turbulent” viscosity coefficient [see Dosanjh et al. (1962), Squire (1965), Ogawa (1993) and Bhagwat & Leishman (2000a, 2002)], where now the assumption is that rc{t) = f4ctEvt. The coefficient S takes into account the more rapid core growth based on an average increased rate of vorticity diffusion as a result of turbulence generation and is a coefficient that must be deduced from vortex core structure measurements. Squire (1965) has postulated that the effective (turbulent) viscosity coefficient, 5, should be a function of the circulation strength (circulation) of the trailed tip vortex, Г„. Because, in practice, the strength (circulation) of the vortex is conserved and is found to remain nominally constant as the vortex ages in the flow [see Dosanjh et al.

(1962) , Mahalingam & Komerath (1998), and Bhagwat & Leishman (2000a, 2002)] it is reasonable to assume a constant value of S. However, this hypothesis can only be verified through experimental correlation. In addition, because it is known that the vortex is already in some stage of decay immediately after its formation, it can be hypothesized that the growth curve can be originated at a virtual time, say to, so that rc(t) = s/4aSv(t — to) – see Squire (1965) and results in Fig.-10.22.

Equivalent downstream distance, ip Г / Qc2 f(Re )

W V V

Figure 10.23 General correlation of rotor tip vortex measurements in terms of nondimen – sional maximum tangential velocities and nondimensional downstream distance.