A STRUCTURED APPROACH

In the previous subsection, a specific structure was given to the model perturbation Д(а) only a posteriori, so that equations (11.25) and (11.27) are just sufficient conditions of stability of the closed loops of figures 11.5 and 11.6.a.

It is nevertheless possible to introduce scaling matrices in order to re­duce the conservatism of the approach. The model perturbation A(s) is diagonal (see equation (11.22)), so that diagonal scales D(s) = diag(di(s)) commute with the model perturbation, i. e.:

D{s)A{s)D~l{s) = A(s) (11.30)

These scales can thus be introduced in the closed loop of Figure 11.6.a without modifying its stability properties (see Figure 11.6.b). The small gain theorem gives a new sufficient condition of stability at frequency to:

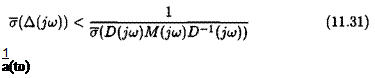Noting:

min <r(D(jto)M(jto)D 1(ju;))

D(ju)

less conservative values of the MIMO phase and delay margins can be computed with equations (11.25) and (11.27). The issue is to minimize at frequency to the quantity:

with respect to invertible and diagonal real and positive scaling matrices D(juj). This is the same problem as in subsection 2.2 of chapter 5 (com­putation of acomplex ц upper bound). (Sub)optimal solutions to this op­timization problem can be found in the ц Analysis and Synthesis Toolbox or in the Robust Control Toolbox (the routinepsv. m of this last Toolbox is especially efficient).