Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
AN IMPROVED ALGORITHM
The issue is to compute the robust delay margin, i. e. the minimal value of the MIMO delay margin when Ді belongs to its unit ball. The following algorithm, which is to be applied at each frequency u>, will be used in the following section:
1. 
Computation of an upper bound of typically the mixed
H upper bound of (Fan et al., 1991). If it is greater than 1, stop. It is indeed impossible to guarantee that the closed loop without time delays is stable when the classical model uncertainties in Д i belong to the unit ball.
2. Computation of a lower bound of the robust delay margin using the small gain approach of section 3. and a direct model perturbation. If an infinite margin is obtained, stop.
3. Computation of a lower bound of the robust delay margin using the small gain approach of section 3. and an inverse model perturbation. If an infinite margin is obtained, stop.
4. The method of section 2. is applied.
Remark: Steps 2 and 3 are performed before Step 4 because they are computationally less involving. Their purpose is to eliminate the frequency points, for which the margin is infinite.
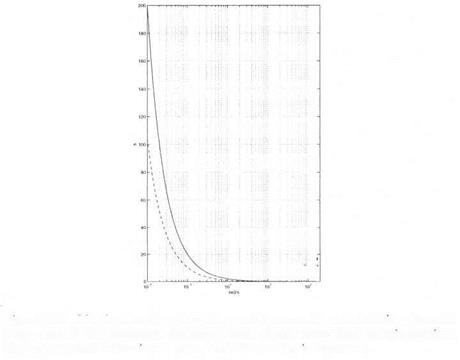
Missile example with 3 delays and 4 parametric uncertainties – the solid
(resp. dashed) line represents the lower bound of the robust delay margin obtained with the approach of section 2. (resp. with the small gain approach).
