Eddy viscosity
Away from the immediate influence of the wall which has a damping effect on the turbulent fluctuations, the Reynolds shear stress can be expected to be very much
greater than the viscous shear stress. This can be seen by comparing rough order – of-magnitude estimates of the Reynolds shear stress and the viscous shear stress, i. e.
-Г7 e da
p uV c. f. tidy
Assume that u’v’ ~ CU^ (where C is a constant), then
showing that for large values of Re (recall that turbulence is a phenomenon that only occurs at large Reynolds numbers) the viscous shear stress will be negligible compared with the Reynolds shear stress. Boussinesq[40] drew an analogy between viscous and Reynolds shear stresses by introducing the concept of the eddy viscosity Єт-
r — Q —
T = /i^ cf. – piSV = рєтщ: £T^>v{=p/p) (7.109)
Boussinesq, himself, merely assumed that eddy viscosity was constant everywhere in the flow field, like molecular viscosity but very much larger. Until comparatively recently, his approach was still widely used by oceanographers for modelling turbulent flows. In fact, though, a constant eddy viscosity is a very poor approximation for wall shear flows like boundary layers and pipe flows. For simple turbulent free shear layers, such as the mixing layer and jet (see Fig. 7.35), and wake it is a reasonable assumption to assume that the eddy viscosity varies in the streamwise direction but not across a particular cross section. Thus, using simple dimensional analysis Prandtl^ and Reichardt* proposed that
єг= к x AU x 6 (7.110)
const. Velocity difference across shear layer shear-layer width
к is often called the exchange coefficient and it varies somewhat from one type of flow to another. Equation (7.110) gives excellent results and can be used to determine the variation of the overall flow characteristics in the streamwise direction (see Example 7.9).
The outer 80% or so of the turbulent boundary layer is largely free from the effects of the wall. In this respect it is quite similar to a free turbulent shear layer. In this
|
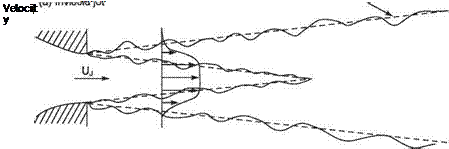 |
Uj Inviscid Jet boundary
V
Mixing-layer region
(b) Real turbulent jet
Fig. 7.35 An ideal inviscid jet compared with a real turbulent jet near the nozzle exit
outer region it is commonly assumed, following Laufer (1954), that the eddy viscosity can be determined by a version of Eqn (7.110) whereby
![]() єт = nUe6*
єт = nUe6*
Example 7.9 The spreading rate of a mixing layer
Figure 7.35 shows the mixing layer in the intial region of a jet. To a good approximation the external mean pressure field for a free shear layer is atmospheric and therefore constant. Furthermore, the Reynolds shear stress is very much larger than the viscous stress, so that, after substituting Eqns (7.109) and (7.110), the turbulent boundary-layer equation (7.108b) becomes
The only length scale is the mixing-layer width, S(x), which increases with x, so dimensional arguments suggest that the velocity profile does not change shape when expressed in terms of dimensionless y, i. e.
This is known as making a similarity assumption. The assumed form of the velocity profile implies that
![]() _yjdA
_yjdA
Sdx)
dq/dx where F'(rf) = dF/drj.
Integrate Eqn (7.108a) to get
v =
so
6 f
v=Uj — G{rf) where G — I rjF'(rj)drj
The derivatives with respect to у are given by
дй=дп*й=Ц1
dy dydV S w
cPu _ dr] d /<9w dy2 dydr) dy)
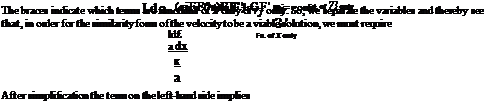 |
The results given above are substituted into the reduced boundary-layer equation to obtain, after removing common factors,
— = const. or a OC X dx
Setting the term, depending on 77, with F" as numerator, equal to a constant leads to a differential equation for F that could be solved to give the velocity profile. In fact, it is easy to derive a good approximation to the velocity profile, so this is a less valuable result.
When a turbulent (or laminar) flow is characterized by only one length scale – as in the present case – the term self-similarity is commonly used and solutions found this way are called similarity solutions. Similar methods can be used to determine the overall flow characteristics of other turbulent free shear layers.











