Harmonic Oscillations of a Thin Foil in a Two-Dimensional Flow

Consider a thin foil advancing near the ground with a constant speed U0 and simultaneously performing small vertical motions (heave, pitch or deforma­tions). An unsteady wake, consisting of the shed vorticity, is formed behind the foil in the process of such a motion. According to the general scheme discussed previously, the channel flow in this case will be described by the following relationships:

Щ (x, t) = tp*(x, t) + 0(h2),

where

4> – 4> (x, 0 = 4>h (x,0 + h In (x, t) + h(f3 (ж, t),

as is a function of the order of О(є//і), characterizing the vertical component of the flow velocity given on the foil.

The solution of equation (3.85) can be written in the form

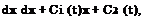
(3.86)

where C(t) and C^t) are the functions of time to be determined with the help of the boundary conditions for the channel flow potential at the leading and trailing edges.

(0 ,**)>

dt*2

The lowest order induced unsteady downwash in the wake can be deter­mined by using the formula

where t* = t + x. In the case of harmonic motions,

(0, t*) = acoskt* + bsin/cf*, aWl = — к2(рг (0, £*),

where a and b are constants determined in the course of solving the lowest order problem, к = loC0/U0 is the Strouhal number, and и is the circular frequency of the unsteady process.

In the upper flow, the corresponding asymptotic expansion for the velocity potential has the form

<Pu = htpUl + o(/i2 In i).

Solution (рг is constructed by distributing along a semi axis x < 1 sources (sinks) whose strength is equal to the doubled local downwash, which is
given on the foil and determined in the wake. At the leading edge, we place an admissible point source (sink) solution that does not violate the flow tangency conditions either on the foil or in the wake. Thus, at points on the upper surfaces of the foil and the wake

= 2тг ІП^ ~ + 2^ / q^ ln(X ~ ® d^’ (3-87)

where

t = і -2as(x, t), 0 < x < 1;

^ — 2aWl(x, t), — oo < x < 0.

Note that the strength of the point source (sink) at the leading edge has to be determined by matching. Note that when calculating (pUl with the help of (3.87), the following integrals are encountered:

These integrals are divergent in the conventional sense. Nonetheless, they can be calculated in a generalized (Abel-Poisson) sense; see Fikhtengoltz [135].

poo

I — lim / exp(—<5£) cos k( In £

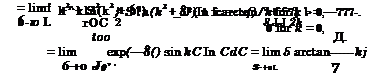Jo

where 7 ~ 0.5772 – the Euler constant.

From a physical viewpoint, the generalized integration means that we consider slowly amplifying oscillations, turning in the limit into oscillations with constant amplitude. An analogous approach was used by Theodorsen in calculating integrals of the type

in the work on harmonic oscillations of a thin foil in an unbounded flow. Taking into account (3.88) and (3.89), the expression for <pUl can be rewritten as

Q, n = – ln(l-z

<Xs(Z, t) ln(z-0 d£

к

+ — [(aG і + bG2) cos kt + (bGi — aG2) sin fcfc],

7Г

where

G—L cos kx + M sin fcx, G2 = L sin kx — M cos fcx;

L = si(fcx) — sin kx In x, M = 2 In fc + cos kx In x — ci(fcx).

Functions si(fcx) and ci(fcx) are integral sine and cosine, defined by the ex­pressions

To match, one needs to know the asymptotic expansions of (pUl near the edges. These were found in the form

• Near the leading edge (у — x — 1 —> 0)

Q, , <*s(M) , , Axv A2

ipu, – х-шьЧ————– V in v——– 1——- 1- 0(v )

27Г 7Г 7Г 7Г

A2 = – f as(£,t)n(l-(;) d£+k[(aGn+bG2i) coskt+(bGn-aG2i) sinkt], Jo

where Gn = Gi(l) and G21 = G2(l).

Near the trailing edge (v = —x —* 0),

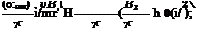V? U;

(o! Uw) —

■Bi = ^Q-as(0,t)- f [as(£, i) — as(0, i)] ^ + fc{[a(fcG2o — 1) — bfcGio] cos kt
+ [6(fcG2o — 1) + afcGio] sin kt}]

B2 — — o;s(£, 0 In £ d£ + fc[(aGio + bG2o) cos kt + (bGw — UG20) sin kt],

Jo

Glo = G1(0) = ~ G2o = G2{0) –

The following results can be obtained from matching the solutions determined in the upper, channel, and edge regions.

Constants of the local solution at the leading edge (x = 1):

1

а і

a3 = ^ Ai+ «s(l, t) (l – In ^ , a4 = і (a2 – оц In ^). • Constants of the local solution near the trailing edge (x = 0):

£i + <auw)(i-ln0], b+ = ^B2.

Application of the Kutta-Zhukovsky condition at the trailing edge (v — —x/h = 0) gives a relationship between, fcj" and bj, 63":

db3 , dbt lr / 7r

b2+~dT~b2 + ^-n[Bl + M1~lnh) +

Boundary conditions for the equation (3.85):

At the leading edge,

¥>l(l,0 = ^ m — «1 (1+ In ^)

At the trailing edge (x = 0),

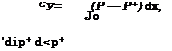As a result of matching, additional information was obtained that provides uniqueness of the asymptotic solutions, determined in different regions of the flow. Forming uniformly valid (additive) composite expressions for the pressure coefficient on the upper p+ and the lower p~ surfaces of the foil and integrating these expressions, we obtain formulas for the lift and moment coefficients

where

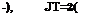
dx dt / V dx dt 1

As a first example, consider heave oscillations of a flat plate, for which in­stantaneous positions with respect to the ground are described by the equa­tion

ys = h + h0 sin kt,

whereas the vertical downwash on a plate

The lift coefficient was obtained with an asymptotic error of the order of О(h2) in the following form:

Cy = hC* + hC$,

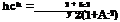
h 1 2(1 + k2)2 + 2 – k2 7ГІП h (1 + A;2)2

h 2-k2 h l(l-k2)(2 + k2) y 6(1 + A:2) + 7Г ft (1 + A;2)2

h f 2(1 + 1п7г) — 2k2 1п7г(2 + к2) — k2[2kGn + (к2 — 1)G2i]

+^l 2(1 +A:2)2

where

Gїї = Gi(l) = si(fc) cos к + [2 In к — ci(fc)] sin fc;

G21 = G2(l) = si(fc) sin fc — [2 In fc — ci(fc)] cos fc.

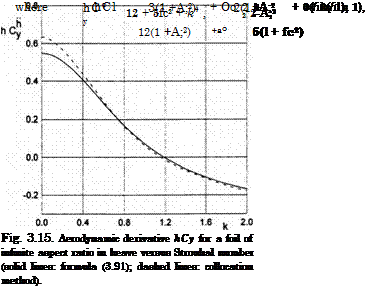
The solution obtained here is valid for a small clearance (/i < 1) and a large range of Strouhal numbers fc C l//i. Some calculated results based on formulas (3.91) and (3.92) are presented in Figs. 3.14 and 3.15.

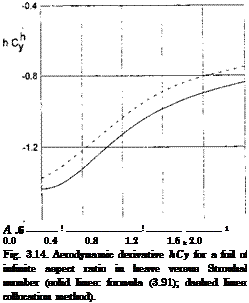On the same graphs are plotted the numerical results of Efremov [104], obtained by the discrete vortex method for h = 0.1. In a similar manner

it is possible to derive formulas for the aerodynamic derivatives for pitch oscillations around a point with abscissa a0 and oscillations of a flap around a hinge point. For briefness, the corresponding expressions for aerodynamic coefficients will be written only for the extreme ground effect (leading order):

• For pitch oscillations,

Cy = 901 + 90°,

• For oscillations of the flap,

Су = efCf + efCey<, (3.94)

hCef = 2bt – bj + k[1 – bf + bf2(6 – 4)/12] – k^jl + 3bf)/6 | 1

y 1 + k2 hh

,, = h(2bf — 2bf/3 — 1) + (1 — bf/2) + 0(Ып 1

1 -(~ к гь

The solution obtained above for the general case of harmonic perturbations is valid both for oscillations of the foil as a solid body and for deformations of the foil.