Incompressible Boundary-Layer Theory

We now carry out a detailed solution for one of the most important viscous-flow problems in aerodynamics—namely, the high-Re-number flow over a flat plate. The analytical technique demonstrated for the flat-plate problem is the key to under­standing a wide variety of other engineering solutions. Clearly, something special is needed to handle the nonlinear (i. e., convective acceleration) terms still present in the momentum balance. This means that the methods of differential-equation theory do not apply. Separation of variables and superposition are no longer appli­cable tools. A method of great utility in such situations is introduced, which often is called the similarity method.

By a flat plate, we mean a surface on which there is no impressed pressure. The governing equations are those shown in Eq. 8.37 without the pressure gradient in the x-direction. That is, both components of the pressure gradient are now zero:

du + dw dx dz

du dw dzu

u— + w— = v—-.

dx dz dz2

This special case was first solved in 1907 by Blasius, a graduate student of Prandtl, at Gottingen University. A solution to Eq. 8.38 is sought that satisfies the no-slip requirement at the surface and matches the flow field at great distance from it. In mathematical form, we require that:

u = Ue(x) for x > 0, z ^ «= u = V^ for x = 0, z > 0.

A major difficulty in carrying out this solution is that the momentum equation is nonlinear. Students undoubtedly have noticed that the nonlinearity is associated with terms arising in the convective acceleration part of the momentum balance. Classical methods for solving partial-differential equations (e. g., a separation of variables) are not applicable in this problem. Also, we lose the ability to superimpose simple linear solutions in representing more complex cases, a technique exploited many times in preceding chapters. Therefore, we must approach this problem differently than in the more conventional situations that arose in the Couette and Poiseiulle flows and in the potential flow problems addressed previously; these were linear problems.

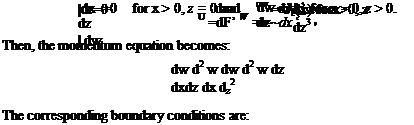A useful step is to reduce the number of dependent variables by using a stream function to represent the velocity field. The continuity equation is satisfied exactly if we write:

Modern computational techniques (i. e., CFD methods) are used routinely to solve nonlinear problems of this type. However, we want to demonstrate a powerful tech­nique that uses mathematical finesse rather than computational brute force to give the required answers. Recall that much physical insight can be gained by using this
approach in place of the “black-box” computations in difficult problems. The price of these benefits is mastery of special mathematical methods not often taught in undergraduate programs (and seldom even in graduate engineering programs). The method introduced often is called the similarity method. It has widespread appli­cation in the solution of nonlinear problems and is strongly couched in simple geo­metrical ideas.