Linear Doublet Distribution

Consider a doublet distribution along the x axis with a strength ц(х) = fi0 + fi,(x — xx), consisting of elements pointing in the z direction [ц = (0, /х)], as shown in Fig. 10.12. In this case, too, only the linear term (ц(х) = цхх) is

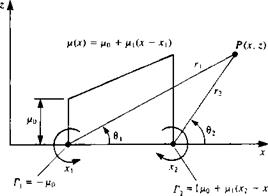FIGURE 10.12

Linearly varying strength doublet element.

considered and the influence at a point P(x, z) is an integral of the influences of the point elements between xl—*x2-

4 -/*1 Ґ2 *0* Ф(ДС,2)“ 2л і, (*-*о)2 + *2 °	(10.56)
/ Ч /*1 Ґ2 *о(* – X0)z л__ и(Х’ } Я І, [(*-*o)2 + z2]2^0	(10.57)
/ ч -/*і Г2[(* -*о)2-*2К j W(X, Z) ~ 2Л і [(*-*0f + z22dXo	(10.58)
The integral for the velocity potential is similar to the w velocity component of the linear source (Eq. (10.46)). Therefore, following Eq. (10.49), the result is
ф*^[2,№-ад+2|п^]	(10.59)

and in cartesian coordinates

2*(tan 1———– tan 1——— ) x-x2 x—xx)

To obtain the velocity components we observe the similarity between Eq.

(10.59) and the potential of a constant-strength vortex distribution (Eq. (10.37)). Replacing /2, with – y in Eq. (10.38) yields

ф’ ‘ [2<J: “ ‘■>,an ^ "2<jr “,г) ,an" ^+2

(10.38a)

and therefore the potential of the linear doublet distribution of Eq. (10.60) is

Ф = ф* *

+ ^(хів1-х2в2)

(10.61)

and the two last terms are potentials of point vortices with strengths [xlxl and (see Eq. (10.8)). The velocity components therefore are readily available, either by differentiation of this velocity potential or by using Eqs. (10.39) and

(10.9) :

z z I

——– tan 1———

X—X2 JC-XjJ

/*1*2 г___________ /*1*1 г

2л (x – x2)2 -I – z2 2л (х – xt)2 + z2

and for the w component using Eqs. (10.40) and (10.10)

= _/*i (* *г)2 z2 /*i*i *~*i /*i*2 * *2

W 4л П (jc -*i)2 + z2 2л (j:-Xi)2 + z2 2л (x – x2)2 + z

The values of the potential and the velocity components on the element (z = 0±, Xi<x<x2) are

Ф = ^~rX 2	(10.64)
-r Ml	(10.65)
A*i Г. (x-x2)2 2×1 2×2 1 W 4jt L П(х – хг)2 x — Xi x — x2l	(10.66)

^1 f*2+*ll Jt lx2 — JCi J

and the w velocity component at the center of the element becomes

(10.66a)

and the velocity is singular at the panel edges because of the point vortices there.

Note that for the general element, where ц(х) = fi0 + Pi(x – *1), the potential becomes

ф=ф** “ ё ■(0z _ ві)+й(Xi ~Хг)вг (10-67)

and due to the potential jump at the edges of this doublet distribution two concentrated vortices exist. The vortex at xt will have a strength of -/r0 while the one at x2 will have a strength of [fii(x2 – x^ + ц0], as shown schematically in Fig. 10.12.