Linear Vortex Distribution

In this case the strength of the vortex distribution varies linearly along the element

У(*) = Уо + Уі(*-*і)

Again, for simplicity consider only the linear portion where y(x) = ylx and y{ is a constant. The influence of this vortex distribution at a point P in the x-z plane is obtained by integrating the influences of the point elements between

Xi~>x2:

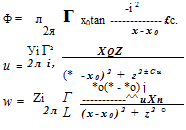(10.68)

(10.69)

Уі [xz, r z, N x2-x2-z2„ x2-x-z2 ф = — hr ln4 + o (*!-**)+———————— о——– ві————- о——-

Using the integral in Appendix В (Eq. (B.18)):

The velocity components are similar to the integrals of the linear source (Eqs. (10.51) and (10.52))

и = zln{*~X’l + Zl-2x(tan_1 ——————— tan’1 – Ml (10.72)

4 лі (x-x2) +z2 x-x2 x-xxJl

■-—)]

X — Ху/J

(10.73)

When the point P lies on the element (z = 0±, x{<x <x2), then Eq. (10.71) reduces to

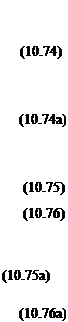Ф=±^(х2-х2)

4

At the center of the element this reduces to

Ф = ±¥±(х2ї + 2х1х2- 3×1)

Also, on the element

and at the center of the element (above +, under -):

W = ±^(*l+X2)

w = -%z(x1-x2)