Mixed boundary layer flow on a flat plate with zero pressure gradient

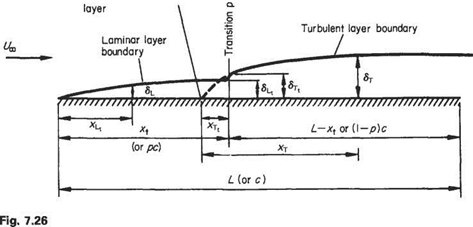
Figure 7.26 indicates the symbols employed to denote the various physical dimen­sions used. At the leading edge, a laminar layer will begin to develop, thickening with distance downstream, until transition to turbulence occurs at some Reynolds number Ret = Uxxt/v. At transition the thickness increases suddenly from <$l, in the laminar layer to &rt in the turbulent layer, and the latter then continues to grow as if it had started from some point on the surface distant xjt ahead of transition, this distance being given by the relationship

0.383лгт,

for the seventh-root profile.

The total skin-friction force coefficient Cf for one side of the plate of length L may be found by adding the skin-friction force per unit width for the laminar boundary layer of length xt to that for the turbulent boundary layer of length (L — xt), and

dividing by where L is here the wetted surface area per unit width. Working

in terms of Reu the transition position is given by

= —Ret

U OC

The laminar boundary-layer momentum thickness at transition is then obtained from Eqn (7.70):

The corresponding turbulent boundary-layer momentum thickness at transition then follows directly from Eqn (7.83):

The equivalent length of turbulent layer (xT,) to give this thickness is obtained from setting ви = вТі – using Eqn (7.93) and (7.94) this gives

/ 1/2 / 1/5

leading to

4/5 0-646 (

Kj’ 0.037 V

*Tt = 35.5 -^Re*/8

U OO

Now, on a flat plate with no pressure gradient, the momentum thickness at transition is a measure of the momentum defect produced in the laminar boundary layer between the leading edge and the transition position by the surface friction stresses only. As it is also being assumed here that the momentum thickness through transi­tion is constant, it is clear that the actual surface friction force under the laminar boundary layer of length xt must be the same as the force that would exist under a turbulent boundary layer of length jcTt. It then follows that the total skin-friction force for the whole plate may be found simply by calculating the skin-friction force under a turbulent boundary layer acting over a length from the point at a distance jcTi ahead of transition, to the trailing edge. Reference to Fig. 7.26 shows that the total effective length of turbulent boundary layer is, therefore, L — jct + *Tt – Now, from Eqn (7.21),

where Cf is given from Eqn (7.85) as

Thus

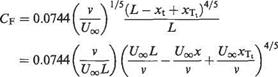Now, Cf = F/^pU^L, where L is the total chordwise length of the plate, so that

i. e.

(7.96)

This result could have been obtained, alternatively, by direct substitution of the appropriate value of Re in Eqn (7.87), making the necessary correction for effective chord length (see Example 7.5).

The expression enables the curve of either Cf or CDf, for the flat plate, to be plotted against plate Reynolds number Re = (U^Ljv) for a known value of the transition Reynolds number Rex. Two such curves for extreme values of Ret of 3 x 105 and 3 x 106 are plotted in Fig. 7.25.

It should be noted that Eqn (7.96) is not applicable for values of Re less than Ret, when Eqns (7.71) and (7.72) should be used. For large values of Re, greater than about 108, the appropriate all-turbulent expressions should be used. However,

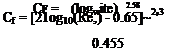Eqns (7.85) and (7.88) become inaccurate for Re > 107. At higher Reynolds numbers the semi-empirical expressions due to Prandtl and Schlichting should be used, i. e.

For the lower transition Reynolds number of 3 x 105 the corresponding value of Re, above which the all-turbulent expressions are reasonably accurate, is 107.

Example 7.5 (1) Develop an expression for the drag coefficient of a flat plate of chord c and infinite span at zero incidence in a uniform stream of air, when transition occurs at a distance pc from the leading edge. Assume the following relationships for laminar and turbulent boundary layer velocity profiles, respectively:

(2) On a thin two-dimensional aerofoil of 1.8 m chord in an airstream of 45 m s_1, estimate the required position of transition to give a drag per metre span that is 4.5 N less than that for transition at the leading edge.

(1) Refer to Fig. 7.26 for notation.

From Eqn (7.95), setting xt = pc

,, = 3

Equation (7.88) gives the drag coefficient for an all-turbulent boundary layer as Cor = 0.1488/ReV. For the mixed boundary layer, the drag is obtained as for an all-turbulent layer of length [x-г, + (1 — p)c. The corresponding drag coefficient (defined with reference to length [хт, + (1 —p)c]) is then obtained directly from the all-turbulent expression where Re is based on the same length [xr, + (1 — p)c]. To relate the coefficient to the whole plate length c then requires that the quantity obtained should now be factored by the ratio

This form of expression (as an alternative to Eqn (7.96)) is convenient for enabling a quick approximation to skin-friction drag to be obtained when the position of transition is likely to be fixed, rather than the transition Reynolds number, e. g. by position of maximum thickness, although strictly the profile shapes will not be unchanged with length under these conditions and neither will Ue over the length.

(2) With transition at the leading edge:

0. 1488

C^=W = °[37]

The corresponding aerofoil drag is then Z)f = 0.00667 x 0.6125 x (45)2 x 1.8 = 14.88 N. With transition at pc, D¥ = 14.86 — 4.5 = 10.36 N, i. e.

CV = x 0.00667 = 0.00465

Using this value in (i), with Res’s = 16480, gives 0.1488

55.8 x 105

5.84 x 10y/8 – 55.8 x 105/> = f55**^5′) ‘ – 55.8 x 105 = (35.6 – 55.

V 0.1488 )

55.8p – 5.84p5/8 = 20.2

The solution to this (by successive approximation) is p = 0.423, i. e.

pc = 0.423 x 1.8 = 0.671 m behind leading edge

Example 7.6 A light aircraft has a tapered wing with root and tip chord-lengths of 2.2 m and

1.8 m respectively and a wingspan of 16 m. Estimate the skin-friction drag of the wing when the aircraft is travelling at 55 m/s. On the upper surface the point of minimum pressure is located at 0.375 chord-length from the leading edge. The dynamic viscosity and density of air may be taken as 1.8 x 10_5kgs/m and 1.2kg/m3 respectively.

The average wing chord is given by c = 0.5(2.2 + 1.8) = 2.0 m, so the wing is taken to be equivalent to a flat plate measuring 2.0 m x 16 m. The overall Reynolds number based on average chord is given by

1.2x55x2.0

= 7.33 x 106

Since this is below 107 the guidelines at the end of Section 7.9 suggest that the transition point will be very shortly after the point of minimum pressure, so ~ 0.375 x 2.0 = 0.75 m; also Eqn (7.96) may be used.

Rex = 0.375 x Re = 2.75 x 106

So Eqn (7.96) gives

CF = ^.°74^ {7.33 x 106 – 2.75 x 106 + 35.5(2.75 x 106)5/8}4/5 = 0.0023

f. j j X 1 и

Therefore the skin-friction drag of the upper surface is given by

D = ^-pU^csCf = 0.5 x 1.2 x 552 x 2.0 x 16 x 0.0023 = 133.8N

Finally, assuming that the drag of the lower surface is similar, the estimate for the total skin – friction drag for the wing is 2 x 133.8 ~ 270N.