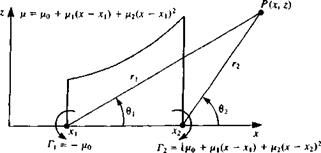
Quadratic Doublet Distribution

As indicated by Eq. (3.150) in Section 3.14 a quadratic doublet distribution is similar to the linear vortex distribution of the previous section. However, in situations when the Dirichlet type boundary condition is applied, it is more convenient to use the corresponding doublet distribution (instead of the linear vortex distribution). Thus, a quadratic doublet distribution along the x axis

FIGURE 10.13 Quadratic-strength doublet element.

(jt, <x <x2) will have a strength distribution of

ИІx) = (*o + Pi(x ~ *i) + – Xyf

where the doublet elements pointing in the z direction [ц = (0, ju)] are selected, as shown in Fig. 10.13. Since the contribution of the constant and linear strength terms were evaluated in the previous sections, only the third term (ju(jc) = (i2x2) is considered and the influence at a point P(x, z) is an integral of the influences of the point elements between xx—*x2:

	(10.77)
, 4 dl Г2 (x-x0)zxl J U{X>Z) Д,[(*-*„ )2 + z2]2dXo	(10.78)
, ч – Рг Г2 [(X – x0f ~ z2x% ^X’Z)~2nl Цх-х^ + г2]2	(10.79)

The integral for the velocity potential is obtained by introducing the variable X=x— x0 (thus dX = — dx0), which transforms Eq. (10.77) to the form

Г~хг(x2-2xX + X2)z 2л X_Xl X2 + z2

The three integrals formed by the terms appearing in the numerator are evaluated in Gradshteyn and Ryzhik,6 3 pp. 68-69, and yield

ф(*> z) = ^ J(x2 – z2)(0! – в2) – xz ln^ + z(Jti – jc2)J

where the variables r,, r2, 6X, and 02 are shown in Fig. 10.13.

Note that Eq. (10.80) can be rewritten as

Ф(*, 2) = Ф** + £-(х21Є1-х22в2)

such that Ф** is the potential of the equivalent linear vortex distribution of Eq. (10.71) (with ц2 = ~УіД).

Ф** = 2л [~XZ ІП% + “Xl) + _ z2^01 ” + 2л^202 “ *201^

(10.81a)

Therefore, Eq. (10.81) states that the potential of a quadratic doublet distribution is equivalent to the velocity potential of a linearly varying strength vortex distribution plus two concentrated vortices at the panel edges as shown schematically in Fig. 10.13.

To obtain the velocity components we can use the similarity between Eq. (10.80) and the potential of a linearly varying strength vortex distribution (Eqs. (10.72) and (10.73)). Replacing ju2 with – ухІ2 in Eqs. (10.72) and

(10.73)

and adding the velocity components of the two point vortices yields

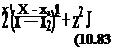and

The value of the potential on the element (z = 0±, Xj <x <x2) becomes

2

Ф(х. 0±) = ^(ві-в2)

and above the element вх — 62 = —л, whereas under the element вх — в2 = л. Consequently,

2

Ф(х, 0±) = T (10.84)

Similarly the velocity components become

u(x, 0±) = ^ (—2x)(02 – Єх) = T/x2x

86)

and the velocity is singular at the panel edges because of the point vortices there.

Note that for the general element, where ju(x) = ц0 + ju,(x – X]) + /і2(х – Xi)2, the potential jump at the edges of this doublet distribution results in two concentrated vortices. The vortex at xx will have a strength of —ц0 while the one at x2 will have a strength of [ju0 + Ц{х2 – Xj) + ju2(x2 – Xj)2], as shown schematically in Fig. 10.13.