Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Quasi-steady force and moment parameterization
Dimensional analysis indicates that all the force and moment coefficients have the following parametric dependence for steady flows. The same dependencies also approximately hold for quasi-steady flows such as an aircraft in slow maneuver.
Cd = Cd(а, в, p, q,r, а, в,5t,5a,5e, Sr, M^,Beao)
Cy = Су (а, в, p, q, Г, а ,в, St, Sa, Se, Sr, MTO, Beoa)
Cn = Cn(a, в, p, q,r, а, в, St,5a,5e, Sr, MTO, Be00)
The parameters St, Sa, Se, Sr are throttle, aileron, elevator, rudder control parameters (there may be more). These represent thrust settings or control-surface deflection angles, which influence the overall force and moment on the aircraft.
 |
 |
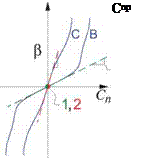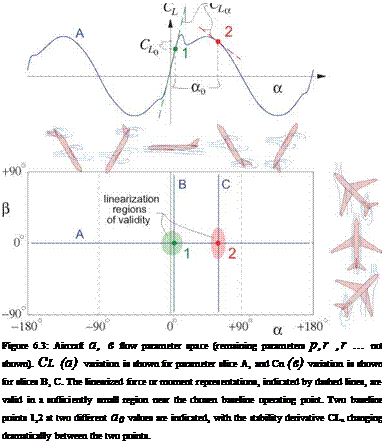
Figure 6.3 shows typical flows over the entire possible а, в range, most of which involve large-scale separation and flow reversal. The result is that the force and moment coefficients have complicated dependencies on the operating parameters, as indicated in the sample CL(a) and Cn(e) line plots in Figure 6.3.
The overall parameter space is enormously larger than the two-axis slice shown in Figure 6.3, since there are additional axes for p, q, r, a,3 ,ST…, MTO, Re. For many applications, such as mission performance estimates, stability and control analysis and design, etc., the force and moment coefficients only need to be defined within a small region of the parameter space, described by small deviations about some operating point or trim state, denoted by the ()0 subscript. Here the force and moment coefficient functions can be approximated by their linearized forms, or equivalently then – first-order Taylor series approximations.
|
Cl |
^ Clo |
+ CLa Aa |
+ CLq |
+ <1 |
CLa A« |
+ CLSe Д5е |
(6.12) |
||
|
Cn |
– Cno |
+ Cne Дв |
+ Cnp |
, ap + |
Cnr A3 |
+ CnSr A$r |
(6.13) |
||
|
where |
|||||||||
|
Clo = |
– CL(ao, eo,. |
..) |
CLa |
= dCL/да |
О О 0, |
••) |
CLq = |
: dCL/dq (ао, во,…) |
|
|
Cno = |
_ Cn(a0,e0v |
..) |
Cne |
= dCn/дв |
0 0 0^ |
..) |
Cnp = |
: dCn/dp (ао, во,…) |
■ ■ ■ (6.14) |
The series variables are the aerodynamic parameter perturbations from the trim state.
Да = a — a0 Aft = в — во Д p = p — p0 … (6.15)
The series coefficients CLa, CLq… are stability derivatives, and Cls, Cngr … are control derivatives. These play a crucial role in aircraft flight dynamics and stability and control, as outlined in Chapter 9. Note that these coefficients can substantially depend on the baseline trim state values, and some may have their signs reversed between different trim states, as for example CLa shown in Figure 6.3.
