Source-Sink Pair

This is a combination of a source and sink of equal strength, situated (located) at a distance apart. The stream function due to this combination is obtained simply by adding the stream functions of source and sink. When the distance between the source and sink is made negligibly small, in the limiting case, the combination results in a doublet.

2.9.2 Doublet

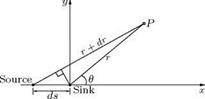
A doublet or a dipole is a potential flow field due to a source and sink of equal strength, brought together in such a way that the product of their strength and the distance between them remain constant. Consider a point P in the field of a doublet formed by a source and a sink of strength q and — g, respectively, kept at a distance ds, as shown in Figure 2.11, with sink at the origin.

Figure 2.11 Source and sink.

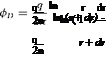By Rankine’s theorem, the velocity potential of the doublet, фо, can be expressed as the sum of the velocity potentials of the source and sink. Thus, we have:

dr

Expanding ln ( 1 +—– ), we get:

But — ^ 1, therefore, neglecting the second and higher order terms, we get the potential function for a r

doublet as:

q dr 2n r

By the definition of doublet, ds ^ 0, therefore:

dr = ds cos в

Hence,

-ds cos в.

Also, for a doublet, by definition, q ds = constant. Let this constant, known as the strength of the doublet be denoted by m, then:

m = q ds

and

In Cartesian coordinates, the velocity potential for the doublet becomes:

m	( x
фо = —	^x2 + y2 J
ФО 2п

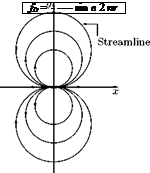Figure 2.12 Doublet with source and sink on the x-axis (source located on the left and sink on the right of the origin). From the above equations for фо, the expression for the stream function fD can be obtained as:

In Cartesian coordinates, the stream function becomes:

ml y

2п У x2 + y2

If the source and sink were placed on the x-axis, the streamlines of the doublet will be as shown in Figure 2.12.

If the source and sink are placed on the y-axis, the resulting expressions for the фо and fD will become:

фО(уу) — 2nr S^n в

m

2п x2 + у2 m

fD(yy) = – 2ПГ cos в

mx 2n yx2 + y2

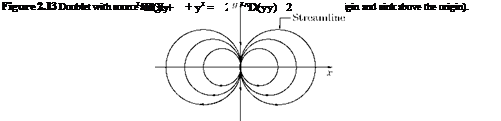
The streamlines of the doublet will be as shown in Figure 2.13. The expression for the stream function:

can be arranged in the form:

fD(yy) = –

where c = m/(2n), is a constant. This can be expressed as:

о о C X

x2 + y + ———- = 0

Thus, the streamlines represented by ^D(yy) = constant are circles with their centers lying on the x-axis and are tangent to the y-axis at the origin (Figure 2.13). Direction of flow at the origin is along the negative y-axis, pointing outward from the source of the limiting source-sink pair, which is called the axis of the doublet.

The potential and stream functions for the concentrated source, sink, vortex, and doublet are all singular at the origin. It will be shown in the following section that several interesting flow patterns can be obtained by superposing a uniform flow on these concentrated singularities.