STABILITY OF CLOSED-LOOP SYSTEMS

We have seen in previous examples how “closing the loop” can modify the basic stability of an airplane. In Sec. 11.4 feedback was used to stabilize an unstable vehicle, and in Sec. 11.5 the addition of a feedback loop to lock on to an altitude or glide reference made a stable vehicle go unstable. We have also seen in the examples how the stability of a linear feedback system can be calculated by formulating the appropriate system matrix and treating it as we would any other linear system.

(b)

Fig. 11.14 (a) Simple feedback system. (6) Single-pulse input: G = Ke~Ts.

For complicated multiloop systems there is relatively little that can use­fully be said in a general way about closed-loop stability. For simple systems, however, as in Fig. 11.14 we can arrive at some general conclusions about the effect of loop gain and phase lag on stability.

CHARACTERISTIC EQUATION

As has been seen in the examples treated, the addition of a feedback loop modifies the characteristic equation, and hence the stability of a system. If the transfer function of Fig. 11.14 is a ratio of two polynomials

N(s)

D{s)

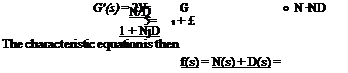then the overall system transfer function is

which is to be eonstrasted with the open-loop equation D(s) = 0. Thus the change in the characteristic equation is produced by the numerator N(s), and the least possible change is the addition of a constant.