. Thin Airfoil Theory (2-D Inviscid Flow)
As seen in class
Ci — 2n(a + 2, Cm, o — _2 (“ + 4
For a given value of camber and Cl, the lift coefficient relation can be solved for the angle of incidence as
Ci d
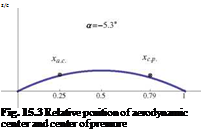
(a)Ci —0.5 — – – 2- — —0.0924rd — -5.3° 2n c
Ci d
(a) Ci —2.0 — – — 2 — 0.1463 rd — 8.4°
2n c
The corresponding moments are
(Cm, o)Ci —0.5 — -0.395 (Cm, o )Cl —2.0 — -0.77
The center of pressure is found from Xf — , that is
(—)q —0.5 — 0.79
ci
(—)Cl —2.0 — 0.385
ci
See Fig. 15.3.
15.2.1.2
 |
 |
Supersonic Linearized Flow (Mo > 1)
The lift coefficient Ci in supersonic flow is given by
Ci (a) = 4 a, where в = ^M — 1.
The moment coefficient is
where (Cm, o)a=0 = | q(f’+(X) + f’ (X))cit.
The thickness distribution has no effect on the moment which reduces to the camber contribution
The moment reads Cm, o(a) = — d. — 2a. The center of pressure is given by
xcp 1 e(Cm, o)a=0 1 + 2 d 1
c 2 4a 2 3 c a











