Thin Airfoil Theory (2-D Inviscid Flow)

15.3.1.1 Incompressible Flow (M0 = 0)

As seen in class, the coefficients for a parabolic camberline are

A2 = ••• = An = 0, n > 2

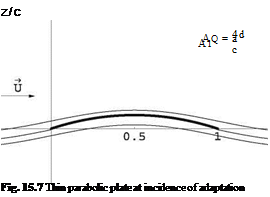
The angle of adaptation or ideal angle of attack is a = 0 since A0 = a. The flow satisfies two Kutta-Joukowski conditions. The leading edge flow has finite velocities. See Fig. 15.7.

The lift coefficient is given by Cl = 2n(A0 + A1/2) = 2n(a + 2d). The incidence of zero lift is thus a0 = -2 = -0.172 rd = -9.85°.

The moment Cm, ac is given by Cm, ac = Cm, o + X~Ci = Cm, o in this case. Indeed: Cm, o = —§ (A0 + A1 – A2/2) = —П – which is the value of Cm, ac for this profile.

The upper limit of the weight (in N) that a wing of chord c = 0.368 m and span b = 4.877 m could lift at Cl = 2 corresponds to the 2-D solution. The lift per unit span is given by

12

L’ = 2pV2c Ci

hence the total lift would be

L = pV2bc Cl = 242.4 N

The corresponding mass at take-off would be M = 24.7 kg.