Two-Degree-of-Freedom Flutter

The analysis of multi-degree-of-freedom systems for determination of the flutter boundary can be demonstrated adequately by the simple two-degree-of-freedom configuration in Fig. 5.2. The equations of motion, already derived as Eqs. (5.26), are repeated here as follows:

m(h + bxe’d) + khh = — L Ip6 + mbxe h + крв = M

where, as before

The next step in classical flutter analysis is to presume that the motion is simple harmonic as represented by

h = h exp(i at) в = в exp(i at)

The corresponding lift and moment can be written as

L = L exp(i at)

M = M exp(i at)

—ш[7]тЬхв h — a2 Ip в + IP а2в = M

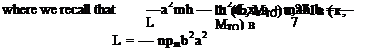Substituting these time-dependent functions into the equations of motion, we obtain a pair of algebraic equations for the amplitudes of h and в in the form

mh (k, MTO) b + me (k, MTO) в

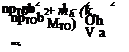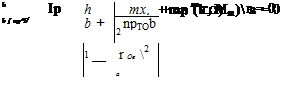Substituting these lift and moment amplitudes into Eqs. (5.58) and then rearranging, we obtain a pair of homogeneous, linear, algebraic equations for h and в, given by

The coefficients in these equations that involve the inertia terms are symbolically simplified by defining the dimensionless parameters used previously; namely

r — A/ m_2 (mass radius of gyration about P)

(pxe + mh) b + pr1 [8]

Using these parameters allows us to rewrite the previous two homogeneous equa­tions in a simpler way:

The third step in the flutter analysis is to solve these algebraic equations for the flight condition(s) for which the presumed simple harmonic motion is valid. This result corresponds to the flutter boundary. If it is presumed that the configuration parameters m, e, a, IP, rnh, юв, and b are known, then the unknown quantities h, в, ю, pTO, Mm, and к describe the motion and flight condition. Because Eqs. (5.62) are linear and homogeneous in h/b and в, the determinant of their coefficients must be zero for a nontrivial solution for the motion to exist. This condition can be written as

The determinant in this relationship is called the “flutter determinant.” Note that the parameter a — a>h /юв was introduced so that a common term that is explicit in ю is available—namely, юв/ю. Thus, expansion of the determinant yields a quadratic polynomial in the unknown X — (юв/ю)2.

To complete the solution for the flight condition at the flutter boundary, it must be recognized that four unknowns remain: юв/ю, p — m/(npTOb2), MTO, and к — Ью/U. The one equation available for their solution is the second-degree poly­nomial characteristic equation from setting the determinant equal to zero. However, because the aerodynamic coefficients are complex quantities, this complex equation represents two real equations, wherein both the real and imaginary parts must be identically zero for a solution to be obtained. This means that two of the four un­knowns must be specified. A procedure to solve for and map the flutter boundary is outlined as follows:

3. Recalling that setting the flutter determinant equal to zero yields a quadratic equation in X, use a root-finding application[9] to find the value of k at which the imaginary part of one of the two roots for X vanishes, which is kF. This can be carried out easily with computerized symbolic manipulation software such as Mathematica™ or Maple™

4. Set mg/mF = т/X(kF) using the root for which X(kF) is real.

5. Determine UF = bmF/kF and MmF = UF/cTO.

6. Repeat steps 3-5 with the value of MCXJF obtained in step 5 until converged values are obtained for MCXJF, kF, and UF for flutter at a given p.

7. Repeat the entire procedure for various values of p (i. e., an indication of the altitude for a given aircraft) to determine the flutter boundary in terms of, say, altitude versus M(XlF, kF, and UF.