Velocity field representation

The overall velocity field relative to the VL configuration at any point r is given by relation (6.18), where the y(s, e) vortex-sheet strength is now lumped into the collection of h. v. filaments, with each filament having a constant strength Гi. The surface integral in (6.17) is therefore replaced with a collection of Biot-Savart line integrals, one for each h. v.

Evaluation of the Biot-Savart integral of the i’th h. v. has produced the V kernel function, given by the following expression. The a and b vectors are shown in Figure 6.7.

if axb /1 1 axx 1 bxx 1 1

47r|a||b|+a-b|a|^|b|y |a| — a • x |a| |b| — b • x |b| / ^ ^

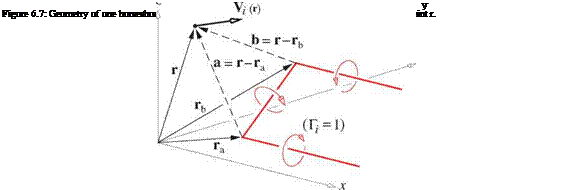The three terms in (6.33) correspond to the bound leg, the ra-point trailing leg, and the гь-point trailing leg, respectively. Note that Vi has units of 1 /length.

6.5.2 Flow tangency condition

The flow tangency condition (6.19) is imposed at the N control points by choosing r in (6.32) to be the control point r/ of each h. v. in turn, and setting the resulting normal velocity component to zero.

To avoid conflict with the control point index i, the summation index over the h. v.’s has been changed to j.

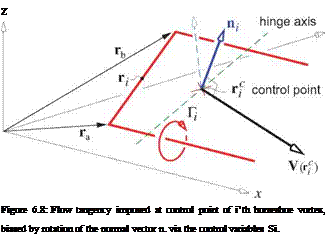
The normal vector ni depends on Si, which are control variables which define the deflections of some number of control surfaces. The control index l = 1, 2 …Ni is more practical for computation than the earlier Sa, Se … notation introduced in Section 6.3.2.

The deflections are modeled by rotating each ni on that control surface about a specified hinge axis. In keeping with the small-angle approximations used throughout lifting surface theory and the VL method in particular, each normal vector’s dependence on Si is linearized. Referring to Figure 6.8 we have

Ni

– noi + E nii Si (6.35)

1=1

= gi hii xnoi (6.36) where hi is the hinge-axis unit vector about which n rotates in response to the Si control deflection, and gi is the “control gain,” included so that the Si control variable doesn’t have to be the actual local deflection angle in radians. To linearize the control influence we will assume that —U/x — V/, x which is equivalent to
а, в ^ 1, and that the normal-vector control deflections щ. Si are small compared to the undeflected normal vector no.. Thus the flow-tangency equations (6.34) are approximated by

Ni

у,(rf) – (U + Oxr£) ■ no. + £ VL X ■ ni. Si = 0 (i = 1. ..N) (6.37)

j=i 1=1

where all products of two small quantities have been dropped.