VORTICITY AND CIRCULATION

The circulation I(c^) in any closed circuit ґ€ is defined by the line integral

І(Щ = f u • dl (1)

where is any closed curve in the fluid, and the integrand is the scalar product of the velocity vector u and the vector dl, which is tangent to the

curve and of length dl (Fig. 12.1). Clearly, the circulation is a function of both the velocity field and the chosen curve.

Using Stokes’s theorem, the line integral can be transformed into the surface integral

m~j{4xu)ndo (2)

where S is any surface in the fluid bounded by the curve e6, provided that there is no discontinuity in the velocity field. The symbol V means the Id Э Э

vectorial operator I — > —> — I. The vector product V X u, some-

d3lj C%2

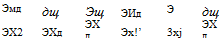times written as curl u, has the following three components in the direction of Xj, Xg, Xg!

If the direction cosines of the outer normal of the surface element do are denoted as пг, n2, n3; then the normal component of the vector V X и is

We define the vorticity at a point in a velocity field as the quantity

X = V x u = curl u (3)

The law of change of circulation with time, when it is taken around a fluid line, i. e., a curve formed by definite fluid particles, is given by the theorem of Lord Kelvin:

Theorem: If the fluid is nonviscous and the body force is conservative, then

Df_ _[ dp Dt J’r p

If, in addition to the above conditions, the fluid is piezotropic, then the last integral vanishes because is a closed curve, and we have the Helmholtz theorem that

(5)

The flow is said to be irrotational if the vorticity is zero throughout the region under consideration.

In the thin-airfoil theory, the conditions of the Helmholtz theorem are satisfied. Hence, the circulation I about any fluid line never changes with

Curve formed by fluid particles that constitute the original curve C-^

Fig. 12.2. Fluid line V enclosing an airfoil
and its wake.

time. Since the motion of the fluid is caused by the motion of the airfoil and since at the beginning the fluid is at rest and I = 0, it follows that I vanishes at all times. Note, however, that the volume occupied by the airfoil is exclusive of the fluid. A fluid line la enclosing the boundary of the airfoil becomes elongated when the airfoil moves forward as shown in Fig. 12.2. According to the Helmholtz theorem, the circulation about ^ is zero, so that the total vorticity inside (<d vanishes, but one cannot conclude that the vorticity actually vanishes everywhere inside. Hence, in the region occupied by the airfoil, and in the wake behind the airfoil,
vorticity may exist, However, the Helmholtz theorem applies to the region outside the airfoil and its wake, and the vanishing of circulation about every possible fluid line clearly shows that the flow is irrotational outside the airfoil and its wake.