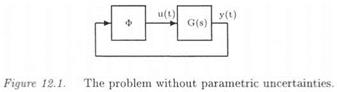
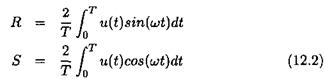2. A GRAPHICAL METHOD
The case of a single SISO nonlinearity is considered. In the first subsection, a classical graphical method for detecting limit-cycles (without parametric uncertainties) is recalled. Subsection 2.2 then proposes an 1The interest of using linear tools (namely Hx control, ц analysis and ц synthesis) in a nonlinear control problem was already emphasized by (Katebi and Zhang, 1995) in a different context.
extension of this method, for detecting limit-cycles in the presence of parametric uncertainties.
2.1 A CLASSICAL METHOD
|
|
Let the closed loop system of Figure 12.1, where Ф represents a SISO nonlinearity and G(s) a transfer function. Assume that y(t) = Xsin(u}t), where X is a positive real scalar. The output of the nonlinearity, which is supposed to have odd symmetry, can be written as:
u(t) — Rsin(ujt) + Scos(u>t) + e(t) (12.1)
where e contains the super harmonic part of signal u. R and S can be computed as:
|
|
The SIDF is introduced as:
N(X, u>) = £±^- (12.3)
It is assumed in this section that the signal e ( Є ) is essentially filtered by the low-pass transfer function G(s) (first harmonic approximation), so that a necessary condition of oscillation of the closed loop is:
|
|
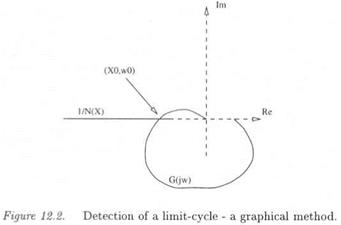
Remark: as a first point, the above equation represents a necessary condition for the existence of a limit-cycle, if the first harmonic approximation is valid. As a second point, when considering a magnitude X0 and a frequency u>o satisfying equation (12.4), the corresponding limit – cycle can be stable or unstable.
|
|
In practice, N(X, u>) generally does not depend on ш, so that equation (12.4) can be solved by looking for the intersection(s) of the plots of G(ju)) and 1/N(X) in the complex plane (see Figure 12.2).