2-D Inviscid, Linearized, Thin Airfoil Theories

15.4.1.1 Incompressible Flow (M0 = 0)

Thickness Effect

In Thin Airfoil theory, the singularity distribution used to represent thickness are sources and sinks.

All the forces and moment coefficients are zero in the symmetric problem asso­ciated with thickness, C; and Cm, o are zero by symmetry, and Cd is zero because it is an inviscid flow theory.

The pressure coefficient Cp is affected by thickness, but the lift, drag and moment integrals are not.

Camber Effect

C; — 2n(a + 2dm) and Cm, o — – n(a + 4dm)/2.

The angle of zero lift is (a)Cl—0 — —2dm.

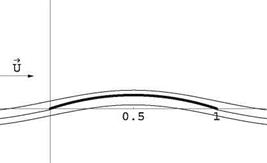
The flow past the mean camber line at a — 0 corresponds to the ideal angle of attack or angle of adaptation. The leading edge satisfies a Kutta-Joukowski condition. The flow is symmetric w. r.t x — c/2. See Fig. 15.9.

z/c Fig. 15.9 Flow past thin parabolic plate at a = 0

Equilibrium About an Axis

At equilibrium the moment about the axis is zero, i. e. Cm, o = 0 ^ a = —4dm = -0.344 rd =-19.7°.

The equilibrium is stable because the slope of the moment about the axis, dCm, o/da, is negative.

At equilibrium, the center ofpressure is at the nose, since xcp/c = – Cm, o/Cl = 0. See Fig. 15.10.

15.4.1.2 Supersonic Flow (M0 > 1, в = yjM( — 1)

Pressure Distributions

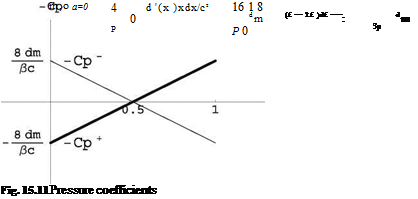
C+ = ^(1 — 2х) and C— = (1 — 2х) at a = 0. See Fig. 15.11.

The corresponding lift coefficient is Cl = 0.

Fig. 15.1( Free body diagram of profile and hinge

Lift and Moment Coefficients

In the general case, C; = pa and Cm, o = -3pdm – pa for a = 0.

Equilibrium About an Axis

The moment about an arbitrary point D along the chord, Cm, D = Cm, o + =

(Cm, o)a=0 – ^1 – 2X^^ 2a. The condition for the equilibrium to be stable is that dCm, D/da < 0. This will be satisfied provided xD/c < 1/2.

The equilibrium incidence is

p. . 4

aeq — 2 Cm, o a=0 / (1 — 2xD/c) — —3dm/ (1 — 2xD/c)

aeq is independent of Mach number.