2-D Inviscid, Linearized, Thin Airfoil Theories

15.5.1.1 Incompressible Flow (M0 = 0)

Definition

In 2-D, the following aerodynamic coefficients C/, Cm, o, and Cd are defined as

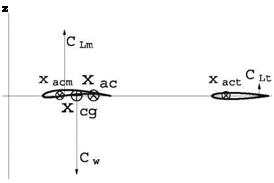Fig. 15.13 Forces locations at take-off

L’ _ M _ D

2 pU2c m’° 2 pU2c2’ d 2 pU2c

The expressions for Cl(a), Cm, o (a) and Cd for a symmetric profile are

Suction Force

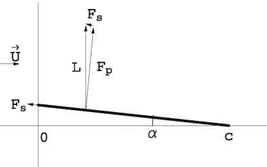
See the sketch of the flat plate at incidence and of the force due to pressure integration and the suction force on Fig. 15.14.

The suction force coefficient can be obtained since the resulting drag coefficient must be zero. Hence

Cs — F’j ^—pU2c^ — Ci sin a = Ci a — 2na2

The thickness distribution contributes to recuperating the suction force by allow­ing the boundary layer to remain attached at the rounded leading edge, thanks to the elimination of the singularity at the sharp trailing edge of the plate.

Center of Pressure

Definition: the center of pressure is the point about which the moment of the aero­dynamic forces is zero.

As seen in class, the center of pressure for a symmetric profile is at the quarter – chord. This is easily shown by using the transfer of moment formula

xcp Cm, o 1

~ = cT = 4

For a symmetric profile, Cm, ac = 0, since the center of pressure coincides with the aerodynamic center (the formula for the value of Cm, ac is the same as that for

Cm, cp.

Computing Cm, o(a) from the Cm, ac, the change of moment formula gives

15.5.1.2 Supersonic Flow (Mo > 1, в = ^— 1)

A thin double wedge airfoil equips the fins of a missile cruising at Mach number M0 > 1 in a uniform atmosphere. The chord of the airfoil is c. The profile camber and thickness are:

d (x) = 0

20x, 0 < x < c/2
2в(е – x), c/2 < x < c

with z±(x) = d(x) ± e(x)/2.

Pressure Distributions

C + and C – are the same at a = 0. One finds

C+ = C – = в в, 0 < x < c/2 C+ = C- = – вв, c/2 < x < c

See Fig. 15.15.

Lift Coefficient

The lift coefficient Ct (a) for all thin airfoils in supersonic flow is only a function of incidence

4

Ct (a) = a

P

Fig. 15.15 Pressure coefficients at a — 0

Drag Coefficient

The drag (wave drag) at zero incidence, (Cd)a=0, is

4 2 4 2

Cd (a) = в2 + a2

в в

Moment Coefficient

The zero incidence moment coefficient (Cm, o) 0 = 0 since it only depends on

camber.

Thus, the values of the coefficient Cm, o for the general case a = 0 is

Maximum Finess

The inverse of the finess, 1/f — Cd/Ci is

в2

1/f = + a

a

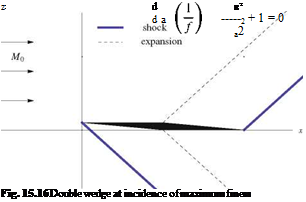and the value of a that maximizes f satisfies

The solution is a = в (a =—в for negative lift). See Fig. 15.16 for remarkable waves (shocks, expansions).