Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
2D unsteady flow interpretation
The sequence of solutions along x can be interpreted as a 2D unsteady flow p(t, y,z) if we make the Galilean transformation
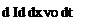x = Vo t
where the new observer is traveling along the x axis at the freestream speed V». The y(s; t), z(s; t) crosssectional shape in the transverse plane and the resulting transverse flow then appear to change in time. In this unsteady interpretation the streamwise perturbation velocity transforms as px ^ pt/VO, which converts the steady 3D Bernoulli equation (6.65) into its 2D unsteady form which gives the same pressure.
P-Pco = ~P<Pt – + <fl)
In practice, when solving the 2D Laplace problem (6.62)-(6.64), the spatial sequence in x or the time sequence in t are computationally equivalent. And for computing the pressure, the 3D steady or the 2D unsteady Bernoulli equations are equivalent as well. Therefore, this transformation and unsteady interpretation does not provide any computational advantages, but it does give some additional insight into the problem.
6.6.3 Local 2D far-field
 |
 |
 |
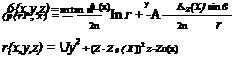At intermediate distances which are large compared to the local body y, z dimension but small compared to the body length l, the perturbation potential must have a local 2D far-field form as given by (2.78).
The vortex term was omitted since there cannot be an overall circulation about this 3D body. The y doublet was omitted by the assumption of left/right symmetry about y = 0, and it can always be eliminated in any case by rotating the axes so that the z axis aligns with the doublet-vector axis. Also, for generality the singularities are placed at some location z = z0(x) rather than at z = 0.
 |
 |
 |
The source strength is related to the body’s cross-sectional area A(x) as derived in Section 2.12.
 |
 |
 |
 |
The z-doublet is related to the lift via the the far-field lift integral (5.50). This requires the pressure, which is obtained from the Bernoulli equation (6.65),
 |
 |
 |
 |
 |
The quadratic terms in (6.65) have been omitted here, since they become negligible at a sufficiently large control volume. Following the procedure in Section C.4, integral (5.50) is now evaluated on a dx-long circular control volume of some radius r, whose arc length element is dl = r d9.
Using (6.69) to calculate the overall lift of the body still requires relating kz to the body geometry, which in general is case-dependent. A simple geometry is considered next as an example.
