Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
CHARACTERISTICS OF DELTA WINGS
Triangular wings with a straight trailing edge (point flying first) are called delta wings, according to their resemblance with the Greek letter A . At least in larger aspect ratios they can be considered to be wings with zero taper ratio (pointed wing tips) and with a swept-back 4 chord line. Such wings would be impractical, however, because of wing-tip stalling and low lift drag ratios at subsonic speeds. Rather, delta wings are primarily designed for supersonic speeds. Their leading edges are highly swept so that the aspect ratio is usually small. Thus, the lift drag ratio at subsonic speeds is low. The leading edges of delta wings are also lateral edges. Circulation around such Ages is obviously different from what was originally meant by that word in two-dimensional flow past airfoil sec:ions; and the flow pattern is essentially different from that of straight wings, within the range of aspect ratios as used in airplanes.
1. CHARACTERISTICS OF DELTA WINGS
In the range of low aspect ratio wings the delta shape is of particular interest. It is used in high speed aircraft, and there is analysis available explaining and predicting at least part of the lift.
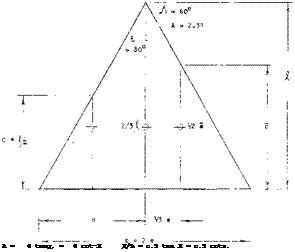
Geometry. Wings in the shape of a delta (with a straight trailing edge) are obtained by combination of sweep and taper. As shown in figure 1, this type of wing is defined by the following parameters:
A = leading edge angle of sweep
€ = 90 – A = half vertex angle
A = 2 Ъ/Я ~ aspect ratio = b2/S
= 4/tanA. for delta wings.
If defining a mean aerodynamic chord in the manner as
Figure 1. Geometry of delta wings, illustrated by the example of an equilateral triangle.
shown for tapered wings in Chapter III, that chord measures c = (2/3)Я. However, since the load distribution of slender delta wings is different from that in conventional planforms, there is no reason to use this type of mean chord. In straight delta wings the length “ У ” would be a natural dimension to define a length ratio. However, to accommodate shapes differing in contour (such as parabolic or “gothic” planforms) the mean geometric chord c = S/b == £ /2 shall be used.
When the trailing edge of delta wings is modified from a straight line the planform is changed to an arrow or a diamond shape as is illustrated on figure 2. For an arrow wing, the wing notch ratio a/f is positive while for the diamond shape a/£ is negative. The notch parameter is used to determine the coefficients for finding the vortex and potential flow lift.
