Constant Doublet Panel Equivalence to Vortex Ring

Consider the doublet panel of Section 10.4.2 with constant strength ц. Its potential (Eq. (10.104)) can be written as

fi f zdS 4л Js r3

where r = V(x – x„)2 + (y – y0)2 + z2. The velocity is

where we have used

JM = д_ _Э _____ Э__1

дхг3~ Эхо г3’ дуг3~ dy0r3

Now, let C represent the curve bounding the panel in Fig. 10.15 and consider a vortex filament of circulation Г along C. The velocity due to the

filament is obtained from the Biot-Savart law (Eq. (2.68)) as

d X r

and for d = (dx0, dy0) and r = (x – x0, у – y0, z) we get

J

z z

■ і 3 <*Уо – j 1 d*o + k[(y – Уо) dxo-(x~ *0) dy0] с г r

Stokes theorem for the vector A is

VXA dS

and with n = к this becomes

dS

Л f Г. 9 z Э z / Э x-x0 д у-уоЧ] An Js L* 9xn r3 1 dy0r3 9×0 r3 9y0 r3

Using Stokes’ theorem on the above velocity integral we get

Once the differentiation is performed, it is seen that the velocity of the filament is identical to the velocity of the doublet panel if Г = ц.

The above derivation is a simplified version of the derivation by Hess (in Appendix A, Ref. 12.4), which relates a general surface doublet distribution to a corresponding surface vortex distribution

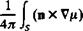f diX

J ^

■>c whose order is one less than the order of the doublet distribution plus a vortex ring whose strength is equal to the edge value of the doublet distribution.