Constant-Strength Vortex Line Segment

Early numerical solutions for lifting flows were based on vortex distribution solutions of the lifting surface equations (Section 4.5). The three-dimensional solution of such a problem is possible by using constant-strength vortex line segments, which can be used to model the wing or the wake. The velocity induced by such a vortex segment of circulation Г was developed in Sections 2.11-2.12 and Eq. (2.68b) states

If the vortex segment points from point 1 to point 2, as shown in Fig. 10.23,

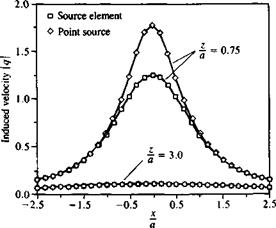FIGURE 10.19

Comparison between the velocity induced by a rectangular source element and an equivalent point source along a horizontal survey line (median).

FIGURE 10.20

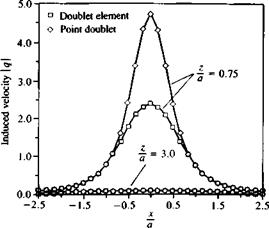Comparison between the velocity in­duced by a rectangular doublet ele­ment and an equivalent point doublet along a horizontal survey line (median).

then the velocity at an arbitrary point P can be obtained by Eq. (2.72):

„ – Г Г1 X r2 (t! Г2

1,2 4я|гіХг2|2Го rj r2)

For a numerical computation in a cartesian system where the (jc, y, z) values of the points 1,2, and P are given, the velocity can be calculated by the following steps:

1. Calculate X r2:

(Гі X r2), = (yp – y,)(zp – z2) – (zp – z,)(yp – y2)
(г, X r2)y = -(Xp – X)(zp – z2) – (zp – z,)(xp – x2)
(ri x r2), = (xp – х^ІУр – y2) – (yp – Уі)(хр – x2)

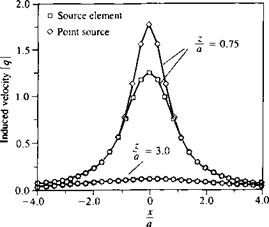FIGURE 10.21

Comparison between the velocity in­duced by a rectangular source ele­ment and an equivalent point source along a horizontal survey line (diagonal).

FIGURE 10.22

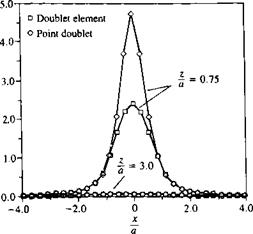Comparison between the velocity in­duced by a rectangular doublet ele­ment and an equivalent point doublet along a horizontal survey line (diagonal).

Also the absolute value of this vector product is

ki x r2|2 = (rt X r2)2 + (г, X r2)2 + (Гі X r2)2

2. Calculate the distances ru r2:

П = У/(хр – x,)2 + (yp – y,)2 + (z„ – zxf r2 = VC*p – X2)2 + (yp – y2f + (zp – Z2f

3. Check for singular conditions. (Since the vortex solution is singular when the point P lies on the vortex. Then a special treatment is needed in the vicinity of the vortex segment—which for numerical purposes is assumed to have a very small radius e)

IF (ru or r2, or Iг! X r2|2 < e)

where € is the vortex core size (which can be as small as the truncation error)

THEN (M = v = w = 0)

or else u, v, w, can be estimated by assuming solid body rotation or any other (more elaborate) vortex core model (see Section 2.5.1 of Ref. 10.3).

4. Calculate the dot-product:

*b * r, = (X2 – x^iXp – Xi) + (y2 – уЖур – Ух) + (z2 – Z)(zp – Zi)

Го r2 = (x2 – Xi)(xp – x2) + (y2 ~ УїХУр – Уг) + (z2 – z^)(zp – z2)

5. The resulting velocity components are

и = X(rt x r2)x v = K(tt x i2)y w = K( rt x r2)2

where

For computational purposes these steps can be included in a subroutine (e. g., VORTXL—vortex line) that will calculate the induced velocity (и, v, w) at a point P(x, y, z) as a function of the vortex line strength and its edge coordinates, such that

As an example for programming this algorithm see subroutine VORTEX (VORTEX = VORTXL) in Program No. 12 in Appendix D.