Equilibrium of the Aggie Micro Flyer (AMF III)

15.5.3.1 Airplane Lift and Moment Curves

The equilibrium code calculated the lift and moment coefficients for the complete configuration at low incidences to be:

CL (a, tt) — 4.47a + 0.37tt + 1.11

См, о(а, tt) — -1.30a – 0.33tt – 0.28

corresponding to AR — 4.9. The main wing aspect ratio is ARm — bm/cm — 8. The difference is due to the wing+tail combination, whereby

amCL m + atCLt

am + at

Therefore, the lift slope and the apparent aspect ratio is a weighted average of the wing and the tail aspect ratios.

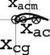
As seen in class, the aerodynamic center xac location is given by

The aerodynamic center is located at xac = 0.29lref = 0.6 m.

15.5.3.2 Equilibrium Incidence

The center of gravity is located at xcg/lref = 0.21.

The static margin is SM = (xac – xcg)/lref = 0.08 = 8%.

The equilibrium incidence a(tt) satisfies the equilibrium equation

CM (aeq) + CL (aeq) = 0

lref

Solving for aeq one obtains

15.5.3.3 Take-Off Conditions

Substituting the previous result in the lift equation provides the equation for the tail setting at take-off

CL, to = 2.0 = 4.47(-0.7tt – 0.13) + 0.37tt + 1.11

Solving for tt one finds tt, to = -0.533 rd = -31°.

The incidence at take-off is therefore ato = 0.24 rd = 14°.

The tail lift coefficient at take-off is CLt, to = 2.49ato + 2.61tt, to – 0.36 = -1.15. The lift force (in N) on the tail at take-off is Lt = 2 pU 2atCu = -12 N.

The force on the tail is down.

15.5.3.4 Extra Credit

Free body diagram at take-off, see Fig. 15.19.

Cw

15.6 Solution to Problem 6