Generalized Radiation and Outflow Boundary Conditions

Radiation boundary condition (6.2) and outflow boundary condition (6.13) were derived for a uniform mean flow in the x direction. In many problems, the mean
flow is not in the x direction. However, if the mean flow is not in the x direction, and even has slow spatial variation, Eqs. (6.2) and (6.13) may be extended to account for a general direction and for a slightly nonuniform mean flow. Let the nonuniform mean flow in the boundary region of the computation domain be (p, u, v, p), then a generalization of radiation boundary condition (6.2) (see Tam and Dong, 1996) is

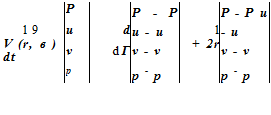
(6.14)

where V (r, d) = u cos в + v sin в + [a2 – (v cos в – u sin в)2]1/2 and a is the local speed of sound. Note: The variables in Eq. (6.2) are the perturbation quantities, whereas (p, u, v, p) are the full variables.

The generalized outflow boundary conditions are as follows:

d u _ 1 d _

— + v ■ v (u – u) = — — (p – p)

dt p dx

9 v _ 1 9 _

— + v ■ V (v – v) = –— (p – p)

91 p dy

where v = (u, v).

It is worthwhile to point out that radiation boundary condition (6.14) allows an automatic adjustment of the mean flow. For time-independent solution, this equation has a solution in the following form:

_ A

(v – v) = Г1/2 ’

and similarly for the other variables. Thus, this set of boundary conditions permits a steady entrainment of ambient fluid when the computed solution requires.