Hypersonic Viscous Interaction

If attached viscous flow is of boundary-layer type, we can treat the inviscid flow field and the boundary layer separately, because we have only a weak interaction between them, Chapter 7.[164] In Sub-Section 7.1.7 we have seen, however, that for large Mach numbers and small Reynolds numbers the at­tached viscous flow is no more of boundary-layer type. We observe in such flows, for instance that past a flat plate, just downstream of the leading edge a very large surface pressure, which is in contrast to high-Reynolds number boundary-layer flows, where the surface pressure indeed is the free-stream pressure. This phenomenon is called “hypersonic viscous interaction”. We use the flow past the infinitely thin flat plate, the canonical case, to gain a basic understanding of the phenomenon.

Hypersonic viscous interaction can occur at sharp-nosed slender bodies and, of course, also at slender bodies with small nose bluntness, i. e., on CAV’s, and can lead to large local pressure loads and, in asymmetric cases, also to increments of global forces and moments. In [47] this interaction is called “pressure interaction” in contrast to the “vorticity interaction”, which is ob­served at blunt-nosed bodies only. We have met the latter phenomenon in the context of entropy-layer swallowing, Sub-Chapter 6.4.2.

The cause of hypersonic viscous interaction is the large displacement thickness of the initial “boundary layer”, which makes the free-stream flow “see” a virtual body of finite thickness instead of the infinitely thin flat plate. Consequently the incoming flow is deflected by the virtual body, a pressure gradient normal to the surface is present, eq. (7.76) in Sub-Section 7.1.7, and a slightly curved oblique shock wave is induced. Actually this shock appears at the end of the shock-formation region (in the classical terminology this is the “merged layer”).

We depict this schematically in Fig. 9.20 [48]. The end of the shock – formation region is characterized by the separation of the emerging shock wave from the viscous flow, which then becomes boundary-layer like. Since the oblique shock wave is slightly curved, the inviscid flow between it and the boundary layer is rotational. In Fig. 9.20 also slip flow and temperature jump are indicated in the shock-formation region. As we will see in Section 9.4, attached viscous flow at large Mach numbers and small Reynolds numbers can exhibit such low density effects.

Before we discuss some interaction criteria, we illustrate the flow phenom­ena in the shock-formation region and downstream of it [49]. The data shown

in the following figures were found by means of a numerical space-marching solution of eqs. (7.74) to (7.77), where the pressure-gradient term in eq. (7.75) has been omitted, because the criterion eq. (7.87) holds

These equations are solved for the whole flow domain including the oblique shock wave, whose structure is fully resolved. This is permitted, because the shock angle в is small everywhere, Sub-Section 6.3.3.

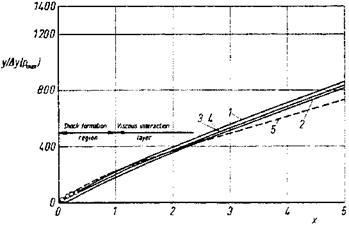
The free-stream parameters are those of an experimental investigation of hypersonic flat-plate flow with argon as test gas [51], Table 9.6.[165] The length of the shock-formation region Lsfr (= L in Fig. 9.20) was found with the criterion eq. (9.47) given by L. Talbot [52], Section 9.4. The stream-wise coordinate x is made dimensionless with it. The viscous interaction region thus is present at x A 1.

Table 9.6. Free-stream parameters of the hypersonic flat-plate argon flow with viscous hypersonic interaction [51, 49]. ДА» ТА [К] Яе’А [1/cm] Ас» [cm] Tw [К] Lsfr [cm] 12.66 64.5 985.45 0.021 285 6.676

The thickness 5 of the computed initial viscous layer can be set equal approximately to the location of the pressure maxima in direction normal to the plate’s surface, which are shown in Fig. 9.21. The Knudsen number, Kn = 5/Аж, then is Kn « 0.125 at x = 0.1 and Kn « 0.0125 at x = 1. Thus also the Knudsen number shows that we are in the slip flow regime for 0.1 A x A 1, and in the continuum regime for x A 1, Section 2.3. In Fig. 9.20 the transition regime—where the flow is becoming a continuum flow— is schematically indicated downstream of the leading edge. In this area the use of the Navier-Stokes equations is questionable, but experience shows that these equations can be strained to a certain degree.

One may argue that strong interaction effects and low-density effects are mixed unduly in this example. However at an infinitely thin flat plate we always have this flow situation just behind the leading edge, even at much larger Reynolds numbers as we have in this case.

Because we are in the slip-flow regime, too, the slip-flow boundary con­ditions, eq. (4.45) in Sub-Section 4.3.1 without the second term, and eq. (4.79) in Sub-Section 4.3.2, are employed. In [49] the influence of the choice of the reflection/accommodation coefficients a and a was investigated, hence the following figures have curves with different symbols, which are specified in Table 9.7. Also the symbols for the strong-interaction limit [53] and the experimental results from [51] are given there.

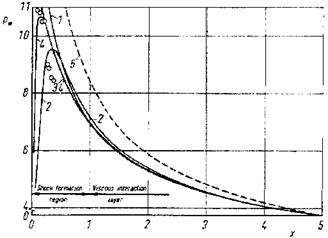
We discuss now some of the results in view of hypersonic viscous inter­action. Fig. 9.22 shows the static pressure pw at the surface of the flat plate non-dimensionalized with the free-stream pressure pTO. The measured data reach in the shock-formation region a maximum of pw « 11, i. e., the pres­sure is there eleven times larger than the free-stream static pressure. The pressure decreases with increasing x in the viscous interaction region. At x

Fig. 9.21. Location of the maximum static pressure in y-direction as function of x = x/Lsfr (Lsfr = 6.676 cm, Ay = 0.00817 cm) [49]. For the symbols see Table 9.7.

Table 9.7. Symbols used in the figures [49]. Symbol a = a 1 і 2 1 – 0.6e-6x 3 0.825 4 0.825 – 0.425e~6Cte 5 strong-interaction limit [53] О experiment [51]

= 5 the pressure is still four times pThe agreement between measured and computed data is reasonably good for the curves 3 and 4, the strong interaction limit lies too high for x ^ 5, which probably is due to the choice of the exponent in the power-law relation of the viscosity in [49].

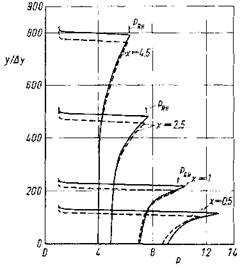
Very interesting are some features of the flow field, in particular the y – profiles of the static pressure p, Fig. 9.23, and the static temperature T, Fig. 9.24, at different x-locations on the plate. The pressure increase from the undisturbed side of the flow (from above in the figure) and the pressure maximum at the top of each curve in Fig. 9.23 indicate for x ^ 1 the high pressure side of the oblique shock wave, which is fully resolved. With the help of the locations of the pressure maxima in the y-direction, Fig. 9.21, the shock angle в as function of x can be determined, too. It is possible then

Fig. 9.22. Non-dimensional static pressure pw(x) at the plate’s surface [49]. For the symbols see Table 9.7.

to compute with eq. (6.86) the Rankine-Hugoniot pressure jump across the shock wave, which is indicated for each curve in Fig. 9.23, too. This pressure jump is well duplicated for x ^ 1. We see also for x ^ 1 the pressure plateau (zero normal pressure gradient) which indicates that the flow there indeed is of boundary-layer type. For x ^ 1 this does not hold. We are there in the shock-formation region, where we even cannot speak of a shock wave and a boundary layer because they are effectively merged.

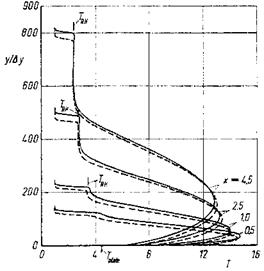
All this is reflected in the у-profiles of the static temperature in Fig. 9.24. The temperature there is non-dimensionalized with TTO. The temperature rise in the shock wave compares well for x ^ 1 with the Rankine-Hugoniot temperature jump, found with eq. (6.85). For x ^ 1 we see also the typical temperature plateau between the (thermal) boundary layer and the shock wave, which coincides with the non-constant portion of the pressure field. In the boundary layer we find the temperature maxima typical for the cold-wall situation, however with the initially strong wall temperature jump which can appear in the slip-flow regime. For x ^ 1, in the shock-formation region, again neither a boundary layer nor a shock wave are identifiable.

The classical hypersonic viscous interaction theory, see, e. g., [47], assumes that a boundary layer exists, whose displacement properties (displacement thickness 5i(x)) induce an oblique shock wave. This means that the boundary layer, downstream of the shock-formation region, is considered as a (convex) ramp, Fig. 6.9, however with a flow deflection angle 5defi which is initially large and then decreases in downstream direction:

dSi. .

tun ddefl = — (x). (9.5)

Fig. 9.23. Profiles of the non-dimensional static pressure p(y) at different locations x [49]. Full lines: a = a = 1, broken lines: a = a = 0.825, RH = Rankine-Hugoniot.

Fig. 9.24. Profiles of the non-dimensional static temperature T(y) at different locations x [49]. Full lines: a = a = 1, broken lines: a = a = 0.825, RH = Rankine – Hugoniot.

The flow deflection angle 5defi can be expressed with the help of eq. (6.114) as a function of the Mach number Mi, the shock angle в, and the ratio of the specific heats 7. We assume small deflection angles Sdefl and small shock angles в, because M ^ 1, and reduce eq. (6.114) to

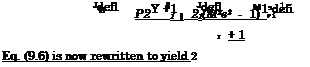Eq. (6.86), which describes the pressure jump across the oblique shock, reads, also for small angles в

We met in Section 6.8 the hypersonic similarity parameter K, which we identify now in the denominator of the last term:

K = M5defl

Solving eq. (9.8) for e/Sdefl, substituting M15defl by K, and putting back the solution with positive sign of the radical into eq. (9.8) gives

In the classical hypersonic viscous interaction theory the pressure p2 be­hind the oblique shock wave is assumed to be the pressure pe at the edge of the boundary layer. In view of Fig. 9.23 this is not correct. The pressure drops considerably in negative у-direction, however downstream with decreas­ing strength, before the plateau of the boundary-layer pressure is reached. Despite this result, we stick here with the classical theory, substitute on the left-hand side of eq. (9.7) p2/p by pe/pand introduce eq. (9.10) to finally obtain the pressure increase due to the displacement properties in terms of the hypersonic similarity parameter eq. (9.9)

We have now to express the boundary-layer displacement thickness Ji, eq. (7.114), in terms of the interaction pressure pe. Assuming flow past an

infinitely thin flat plate at zero angle of attack, we write with the reference – temperature extension, Sub-Section 7.1.6

pOuOx/pO. Without viscous interaction we would have in

Poo, _ T*

* P’I’=Pqo rjl •

P T O

However, with viscous interaction we get

Poo I _ T* p, x

O* ‘pt=p‘ ~ T D *

P T O pe

Following [54] we assume a linear relationship between the viscosity ratio and the temperature ratio

and choose CO according to the boundary-layer situation:

With p = const. in the boundary layer, see Fig. 9.23, we obtain finally the Chapman-Rubesin linear viscosity-law constant

pw TO pxTw

This gives then for the displacement thickness a reference temperature extension of the form

The classical hypersonic viscous interaction theory assumes T*/TO ж M2 [47]. With that we get a Mach number dependence in analogy to the Mach number dependence of the boundary-layer thickness at an adiabatic wall, eq. (7.103)

and its x-derivative

dd ^ Mоо"/ Coo I Poo

dx !!’ .., V /’

In [55] and [56] it is shown, see also [47], that the pressure interaction can be described for two (asymptotic) limits on, for instance, a flat plate. These are the strong and the weak interaction limit. In the strong interaction limit the streamline deflection in the viscous layer is large and hence also the induced pressure gradient across the viscous layer. In the weak interaction limit the streamline deflection is small and hence also the induced pressure gradient.

We treat first the weak interaction limit, where dSjdx is small, hence K < 1, and K2 ^ 1. From eq. (9.11) we get for the pressure, which we interpret now as the induced wall pressure pw:

— = 1 + jK. (9.21)

Рж

With pe к рж and tanSdefi = Sdefl = dS/dx, the hypersonic similarity parameter becomes

.x

It is now called viscous interaction parameter and written either as

or as

.x

For the infinitely thin flat plate we get from [47, 57] the pressure in the weak interaction limit with Pr = 0.725:

This result shows us that the pressure in the weak interaction limit is рж disturbed by a term of approximately 0(x). For the cold wall, Tw/Tt +C 1, and we get with 7 =1.4 for air

— = l + 0.081x. (9.26)

Рж

For the hot wall, Tw к Tt, W. D. Hayes and R. F. Probstein retain a term 0(x2) and arrive at the second-order weak interaction result [47]

In hypersonic flow viscous interaction is a low Reynolds number phe­nomenon, hence we have so far tacitly assumed that the flow is laminar. However in turbulent flow past slender configurations viscous interaction can happen, if the transition location is close enough to the nose region. In this case the interaction parameter for the weak interaction limit reads [58]

1 + 1.3 (Tw/Tt) [1 + 2.5(TW/Tt)]0-6

At the infinitely thin flat plate the pressure in the turbulent weak inter­action limit is, with Pr = 1 and 7 = 1.4

In the strong interaction limit, now again for laminar flow, we have dJi/dx large and therefore K2 ^ 1. Eq. 9.11 becomes then

P^_ = l+ + l) K2 _ 7(7+ Од-2

Pco 2 ~ 2

Because in the strong interaction region pe = pTO, we substitute first of all pTO/pe in eq. (9.19) with the help of eq. (9.30) in order to obtain a relation for Jp

where ReU, = pTOuTO/pTO is the unit Reynolds number. This equation is integrated to yield

(9.32)

respectively

We note in passing that the term in brackets resembles the square root of the co-factors in the у-momentum equation (9.3).

We differentiate now Ji, eq. (9.33), with respect to x and put the result into eq. (9.30) to find finally

pe,l:{ f ‘. oc —

pTO ReTO, x

This results shows that in the strong interaction region the induced pres­sure pe is directly proportional to y, and hence falls approximately oc ж-0’5 in

the downstream direction, see Fig. 9.22. The displacement thickness Si and hence also the thickness of the viscous layer S is ж x0 75, eq. (9.33), compared to ж x0 5 in the weak interaction regime.

The interaction parameter V, arising if the hypersonic viscous interaction effect is described in terms of the pressure coefficient cp, eq. (6.32), is16

which is then combined with eq. (9.34). Finally we consider the consequences of our results. The viscous interac­tion parameters у or К can be employed to check whether strong interaction can appear on a configuration,17 or to correlate locally pressure, skin friction or the thermal state of the surface on both CAV’s and RV’s, see, e. g., [59]. If the check by means of one of the interaction parameters shows that the occurrence of strong hypersonic viscous interaction is likely, numerical or ground-facility simulation must be employed to quantify it to the needed degree of accuracy.18 In ground-simulation facilities this will be a matter of Mach number, Reynolds number and Tw/Tx similarity. Numerical simulation is no problem for laminar flow. If the flow is turbulent, the transition loca­tion can be of large influence, except probably for local hypersonic turbulent viscous interaction effects at inlet ramps etc. [23].

For the infinitely thin flat plate J. H. Kemp obtains for the wall pressure in the strong interaction limit [53]

While applying the interaction criteria one has to keep in mind their x – dependence, which we write explicitly

_ ,i/:; d’. і

у =——————-

/<*’ ;

where xu is the unit interaction parameter.

Strong interaction occurs if is larger than a critical value xcrit■ This can be due to a large value of Ыж combined with a small value of Re^ (Cx usually being of O(1)), or with given Ыж and Re^ for a small value of x. In this case we find the strong interaction limit for x < xcrit, with xcrit being

and likewise the weak interaction limit for x > xcrit.

From eqs. (9.26), (9.27), (9.36), and (9.37) we can deduce critical values for the infinitely thin flat plate in air with 7 = 1.4, if we take p ^ 2 рж as criterion:[166]

— weak interaction:

cold wall: у < Xcrit ~ П, hot wall: у < xcrit « 3,

— strong interaction:

cold wall: у > Xcrit ~ 13, hot wall: у > Xcrit ~ 4.

Applying the hot wall strong interaction criterion to the flat plate case shown in Figs. 9.22 to 9.24, we find with the flow parameters from Table 9.6 the critical length xcrit = 180.1 cm. This, however, appears to be somewhat large in view of the numerical data. We have assumed for argon p ж T0 75, which holds for 50 K ^ T ^ 500 K.

We apply finally the strong interaction criterion to the flow (laminar) past the SANGER forebody, Section 7.3. From Table 7.9 we take the flow param­eters and choose from Fig. 7.10 the wall temperature in the nose region to be Tw « 1,500 K. We find then, assuming p ж t0 65, eq.(4.15), the critical length xcrit = 0.002 m, which shows that no strong hypersonic viscous interaction phenomena are to be expected at the SANGER forebody.