Laminar Separation and Transition to Turbulence

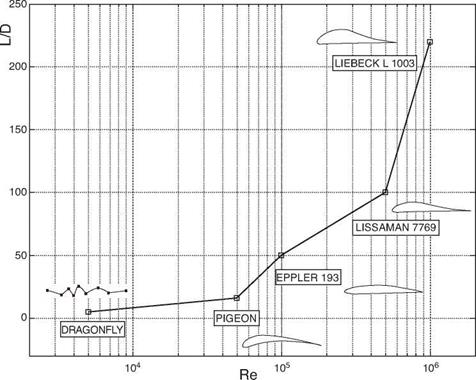
Figure 2.2 illustrates the aerodynamic performance and shapes of several represen­tative airfoils under steady-state free-stream. A substantial reduction in lift-to-drag ratio is observed as the Reynolds number becomes lower. The observed aerody­namic characteristics are associated with the laminar-turbulent transition process. With conventional manned aircraft wings whose Reynolds numbers exceed 106, the flows surrounding them are typically turbulent, with the near-wall fluid capable of strengthening its momentum via energetic “mixing” with the free-stream. Conse­quently, flow separation is not encountered until the AoA becomes high. With low Reynolds number aerodynamics, the flow is initially laminar and is prone to sepa­rate even under a mild adverse pressure gradient. Under certain circumstances, as discussed next, the separated flow reattaches and forms a laminar separation bubble (LSB) while transitioning from a laminar to a turbulent state. Laminar separation can modify the effective shape of an airfoil, and so it consequently influences the aerodynamic performance.

Figure 2.2. Aerodynamic characteristics of representative airfoils. Figure plotted based on the data from Lissaman [21]. Note Re indicates the Reynolds number and L/D indicates the lift-to-drag ratio.

The first documented experimental observation of an LSB was reported by Jones [92]. In general, under an adverse pressure gradient of sufficient magnitude, the laminar fluid flow tends to separate before becoming turbulent. After separation, the flow structure becomes increasingly irregular, and beyond a certain threshold, it undergoes a transition from laminar to turbulent. The turbulent mixing process brings high-momentum fluid from the free-stream to the near-wall region, which can overcome the adverse pressure gradient, causing the flow to reattach.

The main features of an LSB are illustrated in Figure 2.3a. After separation, the laminar flow forms a free-shear layer, which is contained between outer edge S”T” of the viscous region and the mean dividing streamline ST’. Downstream of the transition point T, turbulence can entrain a significant amount of high-momentum fluid through diffusion [93], which enables the separated flow to reattach to the wall and form a turbulent free-shear layer. The turbulent free-shear layer is contained between lines T”R” and T’R. The recirculation zone is bounded by the ST’R and STR.

Just downstream of the separation point, there is a “dead-fluid” region, where the recirculation velocity is significantly lower than the free-stream velocity and the flow can be considered almost stationary. Because the free-shear layer is laminar and is less effective in mixing than in turbulent flow, the flow velocity between the separation and transition is virtually constant [93]. That the velocity is almost

Figure 2.3. (a) Schematic flow structures illustrating the laminar-turbulent transition [93] (copyright by AIAA). (b) Pressure distribution over an SD7003 airfoil, as predicted by XFOIL [96].

constant is also reflected in the pressure distribution in Figure 2.3b. The pressure “plateau” is a typical feature of the laminar part of the separated flow.

The dynamics of an LSB depends on the Reynolds number, pressure distribution, geometry, surface roughness, and free-stream turbulence. An empirical rule given by Carmichael [94] says that the Reynolds number, based on the free-stream velocity and the distance from the separation point to the reattachment point, is approxi­mately 5 x 104. It suggests that, if the Reynolds number is less than 5 x 104, an airfoil will experience separation without reattachment; in contrast, if the Reynolds number is slightly higher than 5 x 104, a long separation bubble will occur. This rule provides general guidance to predict the reattachment, but should be used with caution. As we discuss later, the transition and the reattachment process are too complicated to be described by the Reynolds number alone.

As the Reynolds number decreases, the viscous damping effect increases, and it tends to suppress the transition process or to delay reattachment. The flow will not reattach if the Reynolds number is sufficiently low to enable the flow to com­pletely remain laminar or the pressure gradient is too strong for the flow to reattach.

Thus, without reattachment, a bubble does not form and the flow is then fully separated.

Based on its effect on pressure and velocity distribution, the LSB can be classified as either a short or long bubble [95]. A short bubble covers a small portion of the airfoil and plays an insignificant rule in modifying the velocity and pressure distributions over an airfoil. In this case, the pressure distribution closely follows its corresponding inviscid distribution except near the bubble location, where there is a slight deviation from the inviscid distribution. In contrast, a long bubble covers a considerable portion of the airfoil and significantly modifies the inviscid pressure distribution and velocity peak. The presence of a long bubble leads to decreased lift and increased drag.

Typically, a separation bubble has very steep gradients in the edge velocity, ue, and momentum thickness, в, at the reattachment point, resulting in jumps in Aue and Ав over a short distance. For incompressible flow, the momentum thickness is defined as

в=1′ U (1 – U И <2-d

where u is the streamwise velocity and U is the free-stream velocity. For flow over a flat plate the momentum thickness is equal to the drag force divided by pU[4]. If the skin friction is omitted, the correlation between these jumps can be expressed as

where H is the shape factor, defined as the ratio between the boundary-layer displace­ment thickness S* and the momentum thickness в. The boundary-layer displacement is defined as

delays the transition and elongates the free-shear layer. At this Reynolds number, the separated flow no longer reattaches to the airfoil surface, and the main structures are no longer sensitive to the exact value of the Reynolds number.

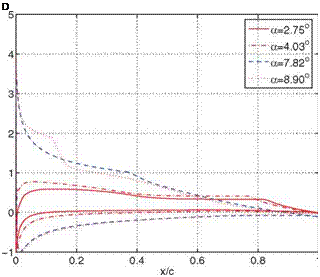
For a fixed Reynolds number, varying the AoA changes the pressure gradient aft of the suction peak and therefore changes the LSB. In this aspect, varying the AoA has the same effect on the LSB as changing the Reynolds number. Figure 2.5 illustrates that, at a fixed Reynolds number of 6.01 x 104for the Eppler E374, a zigzag pattern appears in the lift-drag polar: [5] 2

(c)

3. When the AoA is further increased (beyond 7.82°), the separated flow quickly experiences transition; however, with a massive separation, the turbulent diffu­sion can no longer make the flow reattach, and the drag increases substantially with little changes in lift.

The previously described zigzag pattern of the lift-drag polar is a noticeable feature of low Reynolds number aerodynamics. As illustrated in Figure 2.5, at a sufficiently high Reynolds number, the polar exhibits the familiar C-shape.

Earlier experimental investigations on low Reynolds number aerodynamics were reviewed by Young and Horton [97]. Carmichael [94] further reviewed the­oretical and experimental results of various airfoils with Reynolds numbers span­ning from 102 to 109. In particular, many investigators studied the near-surface flow and aerodynamic loads of a wing at Reynolds numbers in the range of 104 to 106. Crabtree [98] studied the formation of short and long LSBs on thin air­foils. Consistent with the preceding discussion of the two types of separation bub­bles, he suggested that the long bubble directly influences aerodynamic character­istics, whereas the short one serves as an agent for initiating a turbulent boundary layer.

In the last two decades, numerous investigations have been reported on the interplay between the near-wall flow structures and aerodynamic performance. For example, Huang et al. [99] studied the aerodynamic performance versus the surface – flow mode at different Reynolds numbers. Hillier and Cherry [100] and Kiya and Sasaki [101] studied the influence of the free-stream turbulence on the separation bubble along the side of a blunt plate with right-angled corners, finding that the bubble length, sizes of vortices in the separating region, and level of the suction peak pressure can all be well correlated with the turbulence outside the shear layer and near the separation point.