Lifting wings at supersonic speeds

6.8 Consider now the design of lifting wings at supersonic speeds when the attachment lines lie along the leading edges, to extend the discussion in section 6.6 of the corresponding problem at subsonic speeds. The flow we have in mind is one where the bow shockwave is weak and attached to the pointed apex of the wing, and where the shockwave system at the trailing edge has no significant upstream influence and can be regarded simply as the first stage of the process by which freestream condi­tions are regained behind the wing. Viscous effects are confined to these shocks and to the boundary layer which may be assumed to remain attached to the surface forward of the trailing edge, at least at the design point. The disturbance velocities produced by the lifting wing may be assumed to be small compared with the velocity of the mainstream. The local load vanishes along the leading edges. The wing is almost planar and its shape, including the leading edges is smooth. The design Mach number is at once well above the transonic, mixed-flow, range and well below the hypersonic range, where the leading edges would be sonic or supersonic. There is thus no obstacle to the linearisation of the governing equations of motion and of the boundary condi­tions. These circumstances combine to make the situation suitable for the application of the linearised theory of supersonic flow past thin wings and of approximations to it – slender thin-wing theory and not-so-slender thin – wing theory may be adequate in many cases. Thus we discuss theories based on (6.50) or (6.52), as counterparts to those for thick wings in section 6.7.

For aerodynamically slender wings, the relation between the local downwash vz(x, y) and the local load i.(x, y) has already been given in (4.66) and the solution for flat wings in (4.67) to (4.69). For warped wings, the discussion in section 6.6 applies again, and the method of J Weber (1957) can be used.

There are several general methods based on linear thin-wing theory, notably by G J Hancock (1958), G M Roper (1959), and M Fdnain (1961). They use different, but equivalent, forms of the basic downwash equation which replaces (4.49) when the mainstream is supersonic. All involve the differentiation of functions which have to be calculated numerically. This tends to be inaccurate relative to the integration process, and it complicates the numerical analysis by the introduction of a further finite-difference approximation. These matters have been discussed in detail by J H В Smith et al. (1965), who show that these difficulties disappear completely if the order of the calculation can be inverted so that the differentiation operations are carried out

directly on the data and if these are specified analytically. Even if the data are given numerically, the difficulties are removed from the main cal­culation and arise in the initial stage of preparing the derivatives of the data. If the lift distribution vanishes at the leading edges of the wing like the square root of the distance from the edge, a convenient form of the down – wash integral is

where the integration is to be carried out over the Mach forecone, as defined by (6.54) and shown in Fig. 6.60. The discontinuity in the disturbance potential Дф(х, у) is related to the local loading £(x, y) by

£(x, y) = “ "ix дФ(х»У) » (6.73)

and the downwash is equal to the local slope of the mean surface of the wing, as before. The integration operations in (6.72) are conventional. The inte­grand has always a pair of square-root singularities at the ends of the inte­gration interval, whether these lie on the leading edges or the Mach lines.

At the four corners of the curvilinear quadrilateral formed by the leading edges and the Mach lines, these singularities coalesce and simple poles occur. They can be dealt with by classical methods. In the application to the design of the mean surface of a warped wing, it is no effective restriction to require that S,(x, y) or Дф(х, у) be expressed analytically and the differen­tiations in equation (6.72) can then be carried out in closed form. On the other hand, it is important to choose suitable expressions for the loadings to be physically realistic and to correspond to low values of the lift – dependent drag. To express the behaviour at the leading edges, given by у = ±s(x) , in a natural form, the coordinate n = y/s(x) must be introduced. Smith et al. (1965) represented the loading by the product of (1 – n^)i and a polynomial in f whose coefficients are polynomials in x, and this has been proved to lead to an efficient and flexible design method.

Wings with curved subsonic leading edges are not amenable to exact treatment by linear theory, but useful approximations can be provided by the not-so – slender wing theory of Mac C Adams and W R Sears (1953), which has been applied to wings with curved leading edges by L C Squire (1960). He treats both the design of wings to carry a specified load distribution and the cal­culation of the load on wings of specified shape.

There are many useful experimental results from measurements by L C Squire (1959), (1961), (1962), M S Igglesden (1960), C R Taylor (1961), and A L Courtney & A 0 Ormerod (1961), though few include detailed pressure distributions. For one particular wing, J H В Smith et al. (1965) found good agreement between the pressures calculated by linear thin-wing theory and those measured on an uncambered wing at zero lift.

There is now a lift-dependent wavedrag term as soon as Mg > 1 , in addition to the vortex drag. The overall lift-dependent drag can be calculated from the pressure distribution if the latter is also known for the corresponding thick non-lifting wing. The drag calculated by linear thin-wing theory is the same as that found by the supersonic area rule of H Lomax (1955) from

forces in oblique planes through the wing or from "equivalent lineal lift distributions" (see also R T Jones (1952) and E W Graham et at. (1955)). The result can be expanded in a series for small values of Bs/Я. . Mac C Adams and W R Sears (1953) have determined the first term in this series and obtained, for a wing with an unswept trailing edge,

For some special tyes of the function A(l, n) and L(x) , expressions in closed form for the double integrals in (6.74) have been derived by J Weber

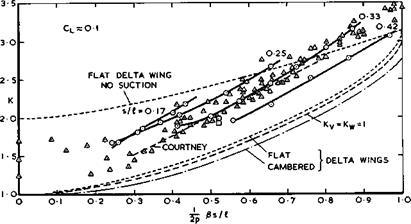
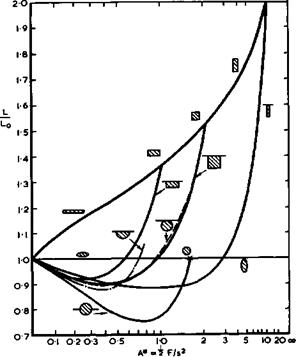
(1957) . Analytic solutions can also be found for other special cases if the condition of zero load along the leading edge is dropped and physically unrealistic infinite suction peaks admitted. When both the integrated chord – wise loading and the integrated spanwise loading are elliptic, a ‘lower bound’ of the lift dependent drag is obtained under the assumption that Bs/J. is small compared with unity, according to R T Jones (1952). This leads to the standard values Ky = Ky = 1 in (3.46) or (4.140), and the drag then increases with Bs/Л as shown in Fig. 6.65. The planforms of flat wings to give such loadings, and especially zero load along the trailing edge (1.(1) = 0) , must have streamwise tips, according to slender wing theory. A flat delta wing has a slightly higher drag, according to linear thin-wing theory. P Germain (1957) and P Germain and M Fdnain (1962) have shown how this can be reduced by the application of warp and an ‘optimum optimorum’ obtained, including the case of a delta wing with nominally sonic leading edges, i. e. Bs/Л = 1 . We see from Fig. 6.65 that the drags obtained by these theories do not differ very much from one another. In general the lift-dependent drag is proportional to and can be reduced by reducing the planform shape parameter p ; that the vortex drag is smaller the larger the value of s/i ; and that the wavedrag increases with both Mach number and s/Л, as indicated in Fig. 6.65 (see also Fig. 4.75).

What really happens can be seen from the experimental values in Fig. 6.65 based on A L Courtney (1960) and J Weber (1976). They all lie above the theoretical curves but below the curve for a flat delta wing with linear lift and no suction along the leading edges, as long as Bs/f. is reasonably small.

LIVE GRAPH

Click here to view

Fig. 6.65 Overall lift-dependent drag factor for uncambered slender wings

This is an indication of the existence of non-linear lift, generated by the leading-edge vortex sheets, and a corresponding drag reduction which is con­sistent with that observed at low speeds (see e. g. Fig. 6.33). This effect becomes weaker as Bs/Л approaches unity and then disappears altogether, which is consistent with the description of the effects of compressibility on the development of the vortex sheets given in section 6.3 (see e. g. Fig. 6.28). The lines through the circles in Fig. 6.65 represent the same family of thick slender wings whose volume-dependent wavedrag is shown in Fig. 6.64. We find that the lift-dependent drag factor varies with the value of s/Л and improves as s/л increases, for given Bs/Л. The triangles in Fig. 6.65 have been taken from data from various sources as collected by A L Courtney (1960). For uncambered wings with streamwise tips, Courtney suggested that

К « Ky + Ку2(Є8/Л)2 = 0.75 + 2.55 Bs/Л (6.75)

gives a good approximation for estimation purposes. This implies that neither Ky nor Кад are strictly constants. Figs. 6.64 and 6.65 together summarise much of what we know about the drag of plane slender wings at supersonic speeds.

The experimental values obtained so far provide some incentive to try to reduce the lift-dependent drag by the application of warp. The aims and methods are much the same as those already discussed in section 6.6. The simplest form of warp is conical camber, and this has been applied with some success to design wings with a relatively low drag, e. g. by J H В Smith &

К W Mangier (1957), G G Brebner (1957) and by V S Holla et at. (1972). In another paper, V S Holla et at. (1972) also evaluate the lift and drag of such wings at off-design Mach numbers. But there is also another design objective of practical importance, and that is to trim the aircraft by means of warp without incurring a significant trim drag.

The problems of balancing and of trirming are fundamental in the design of the kind of slender aircraft in which we are interested here: a tailless

aircraft consisting of a wing of practically constant geometry or of a wing with only a relatively small fuselage (see Fig. 6.7). For the aircraft to be statically stable in longitudinal motion, the increment of lift produced by an increment of incidence must act at or just behind the centre of gravity under all flight conditions. This increment of lift acts at the aerodynamic centre, which is usually furthest forward under the approach condition of low speed and high incidence, so this is where the centre of gravity should be. We have already seen from Fig. 6.51 that the position of the aerodynamic centre at low speeds is always ahead of the centre of area, and the first problem is then to find a planform and a volume distribution which meet the main require­ments of stowage and weight distribution and put the centre of gravity in the right place. The second problem arises from the fact that the centre of pressure on flat wings moves aft as supersonic flight speeds are reached, by as much as 7 or 8% of the overall length, as we have already seen from Fig.

6.24. We want to demonstrate now by some examples how this problem can be solved aerodynamically and the centre of pressure shifted forward at super­sonic speeds by means of warp, following the work of J H В Smith (1959) and J H В Smith et at. (1965) (see also L C Squire (1965)).

A simple way of taking off the extra lift generated in the region of the trailing edge at supersonic speeds would be to defteot trailing-edge flaps upwards. This is a wasteful procedure, as has been shown in calculations by J R Richardson (1957), who compared several delta wings with flaps deflected for trim with a simple, smoothly cambered wing and found that the smooth camber offers a considerable reduction in drag for the same trimmed lift.

This means that warp should be designed to shift the load further forward. According to Munk’s stagger theorem, the vortex drag need not be affected by such a fore and aft shift. But the lift-dependent wavedrag may be changed, as it depends primarily on the lengthwise distribution of the integrated crossload. Other aspects to be considered are the possible introduction of large adverse pressure gradients, which might lead to unwanted flow separa­tions; and also the introduction of large droop angles, which, when combined with large edge angles over the front part of the wing, might hamper the development of non-linear lift (see section 6.4). In general terms, the warp will be designed for a CL-value which is considerably below that reached at low speeds (see e. g. Fig. 6.2) so that it can be expected that the centre of pressure at low speeds will be close to the aerodynamic centre.

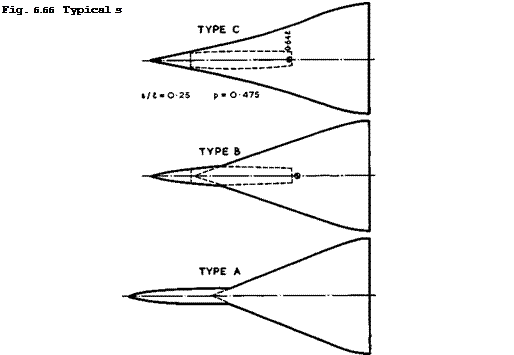
Three possible configurations of a transport aircraft with about 175 seats, for flight at a cruising Mach number Mq = 2.2 across the Atlantic, are shown in Fig. 6.66, as proposed by D Kuchemann & A Spence (1961). Some of the design parameters are given in the table below. All three types are meant to

	Type A	Type В	Type C
V*	0.65	0.78	1 .00
s h	0.24	0.25	0.25
p	0.39	0.45	0.475
6s/A	0.47	0.49	0.49
6s/*w	0.72	0.62	0.49

Some design parameters of the configurations in Fig. 6.66

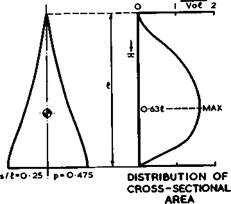
be reasonably realistic and have been designed by J Weber to provide sufficient Volume in the right places. The volume distribution of wing C is shown in Fig. 6.67, which also indicates how the passenger cabin can be accommodated in a bulge within the wing. The volume-dependent wavedrag of this symmetrical configuration is reasonably low: its measured value of Kq was 0.76. The table indicates that Type A may have an advantage over the others because of its low nominal value of p but its wing is no longer aerodynamically slender at cruise. It is not yet known how such a configuration can be trimmed aero­dynamically, and we concentrate here on Types В and C, which may be regarded as slender enough for the application of the design methods discussed above.

The starboard leading edge of wing C is given by

(6.76)

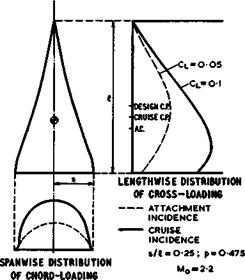
with the centre of area at хса/Л =0.69 . It was estimated at the time of design that the position of the aerodynamic centre at Cl 0.5 and Mq s» 0.2 would be at xac/A =0.64 . The centre of gravity is supposed to be at the same point to give neutral longitudinal stability in the approach. The wing is intended to cruise at Mo = 2.2 and Cl = 0.1 without control surface deflections, with the same position of the centre of gravity. For the sake of achieving a relatively low drag and of moderating the required leading – edge droop, only half the cruising Cl is produced by warp and the other half by an appropriate angle of incidence, as indicated in Fig. 6.68. It is assumed that the two lift and pitching moment contributions are additive.

F(>0t

TYPICAL CROSS-SECTION OF AN UNCAMBERED WING (*=««)

Fig. 6.67 Typical shapes and area distribution of a thick slender wing

Fig. 6.68 Typical spanwise and lengthwise loadings over a warped slender wing

The lift contribution due to the angle of incidence then acts at the high­speed aerodynamic centre which is taken to lie about 8% of the length behind that at low speeds, at xac/£ = 0.72 . The lift contribution of the warp, designed for Cl = 0.05 with the attachment lines along the leading edges, must then act at a point which lies 8% ahead of the aerodynamic centre at low speeds, at xCp/f = 0.56 , so that the combined loading at Cl = 0.1 acts again at x/i. = 0.64 , the centre of gravity.

The warped mean surface of this wing was designed by the method of J H В Smith et at. (1965) described above and details about the many other aspects taken into account in the design may be found in the original paper. The resulting shape is typical for this kind of wing design; it is illustrated in Fig. 6.69,

Fig. 6.69 Mean surface of warped slender wing at attachment angle of incidence

in which cross-sections and chordwise sections are combined to give a three­dimensional impression of the mean surface at its attachment angle of inci­dence. (An isometric projection has been used, where the lengths along chord and span are reduced relative to verticals in the ratio l:/3.) The arbitrary function of у which enters the calculation of the mean surface has been chosen to make the trailing edge straight. The cross-sections show the characteristic droop of the leading edges required to produce attached flow at a positive lift coefficient, with the droop concentrated close to the leading edges towards the rear and spread over the whole cross-section at the front. These cross-sections are arranged lengthwise so that the angle of incidence of the centre line is much larger at the front than at the rear, giving the required shift of the centre of pressure forward from the aerodynamic centre. The mean surface can be described as having negative camber on the centre line, changing through inflected shapes to positive camber near the tips, with marked washout from root to tip. Even with these large changes in wing slope, the local loading f(x, y) still has pronounced peaks inboard of the leading edges and a deep valley along the middle, like those in Figs. 6.57 and 6.58.

Wing C was tested by A 0 Ormerod (1962, unpublished), both as a symmetrical wing and in combination with the warped mean surface described. Some results have been quoted by A Spence and J H В Smith (1962) and by J H В Smith et at.

(1965) and show that this design method can be successful. At the design

Mach number of 2.2, the attachment lift coefficient was produced at an angle of incidence within one-tenth of a degree of the calculated value. At Cjj = 0.05 , the position of the centre of pressure was at xcp/A = 0.57 , i. e. less than 1% of the length behind the intended position. The actual shift in aerodynamic centre between Mq = 2.2; Cl = 0.05 and low speed, Cl = 0.5 , was almost exactly 8% of the length, as assumed in the design. Because the aerodynamic centre of the plane wing at low speeds was about 1% of the length further forward than assumed, and the aerodynamic centre of the warped wing a further 1% ahead of that, the trimmed Cl at Mq *» 2.2 was 0.08 instead of 0.10. At the intended cruising lift coefficient Cl = 0.10 , the measured lift-dependent drag factor was К = 1.93 , which is marginally less than the value of 2.00 measured on the unwarped wing. These values are marked as square points in Fig. 6.65. They are significantly tower than those of a corresponding unwarped wing of delta planform (K = 2.25) or of a thin delta wing with no suction (K = 2.4) . Results very similar to these were obtained with another warped wing designed to have attached flow at Cl = 0 , but to be

trimmed again at Cl = 0.1 . This implies that this method for trimming slender

wings is not very sensitive to the value chosen for the attachment Cl. Differences may arise at off-design Mach numbers, and this makes it possible to consider, and to allow for, conditions at other flight Mach numbers in an actual design, for example, flight at a high subsonic speed.

We have seen from the results in Fig. 6.7 that interest in future designs of supersonic transport aircraft should concentrate on either wings alone or wings with fuselages which protrude only slightly ahead of the wing. With this in mind, the configuration В in Fig. 6.66 was designed. The short fore­body has circular cross-sections, and the sharp-edged wing emerges from the

body side about 30% of the overall length from the nose. Further aft, the body disappears into the wing thickness so that the rear part of the configura­tion can be the same as that of the wing C described above. The volume dis­tribution is such that it can include a cabin with the same number of pas­sengers as that of wing C. We must also bear in mind the discussion of the flow past fuselages and of wing-body interference in sections 5.5 and 5.7 and remember that a round body is a difficult shape on which to produce a chosen distribution of lift of significant magnitude without undesirable uncontrolled flow separations. Therefore, such lift and interference should be designed out as far as possible. A simple way to reduce the interference of the fore­body on the lifting properties of the wing is to arrange the forebody to point into the incident stream at the attachment condition. There is then no body upwash field to interfere with the wing flow and be taken into account in the calculation of the warp distribution. For the distribution of warp to be compatible with this direction of the body, the local angle of incidence of the wing must vanish at the apex. This can readily be achieved in the design method of J H В Smith et al. (1965). The body can then be carried forward from the apex of the gross wing into the wind direction and backward from it along the centre line of the gross wing. The lift carried on the body forward of the wing root is then close to that postulated for the gross wing forward of the same station and, since this lift is small, the correspondence should be close enough for the properties of the wing-body combination to be treated by the methods described for wings alone. Moreover, the upwash generated by that part of the body ahead of the root of the gross wing should also be close to that generated by the portion of the gross wing ahead of the root and should again be small.

A model designed in this way and a corresponding symmetrical model were tested by C R Taylor (1962, unpublished) and some results have been quoted by

A Spence & J H В Smith (1962) and J H В Smith et at. (1965). The attachment lift coefficient of 0.05 was again reached at about one tenth of a degree from the calculated attachment angle of incidence. At Cl = 0.05 , the measured centre of pressure was about 1% of the length of the gross wing behind its intended position. The required forward movement was slightly under-estimated so that the trimmed lift coefficient was again about 0.08. The measured lift – dependent drag factor was К = 1.95 for the warped configuration, as against 2.05 for the symmetrical one, at Cl = 0.10 and Mq = 2.2.

All these results indicate a substantial measure of success for the design procedure and calculation. We may conclude that the trim problem can be solved aerodynamiaally without incurring a trim drag, and that warp can be designed by the methods described as successfully for configurations with short forebodies as for wings alone, provided the bodies can be shaped to fit the flowfield of the wing.

This aerodynamic solution to the trim problem should be the most attractive among the various possible solutions, which include the following: trailing edge flaps may be deflected downwards at low speeds, which can be quite effect­ive but requires complex measures for trimming out by means of a foreplane or of direct jet lift from a special engine installed in front; Kirby’s leading – edge extensions, discussed above, could be an effective means for trimming the aircraft at low speeds when the centre of gravity is put in a position suit­able for cruising flight, but these have not yet been worked out in detail and engineered; lastly, the problem can be circumvented altogether by mechanical engineering in that the centre of gravity is shifted about from one position to another in the manner of the ‘Duke of York’ by pumping fuel fore and aft, as required, during flight.

The methods described so far are intended primarily for the design of relati­vely large transport aircraft. If the slender-wing concept is to be applied to smaller combat aircraft, a fuselage is necessarily more prominent. The volume is then usually asymmetrically disposed about the mean surface of the wing and the fuselage does not fit the flowfield of the wing. The body may generate its own compressions and expansions in the flowfield, and these may be used to advantage in the design if they are superposed on the wing flow in suitable places. For example, expanding flows past bodies placed on the upper wing surface, or compression flows past bodies placed on the lower surface may be used to increase the lift and possibly the lift-to-drag ratio and also for trimming purposes (see e. g. D Kilchemann (I960)), in a similar manner to wing warp, on large and on small wings. How lift and volume effects can be com­bined in a powerful way in the design of non-slender lifting bodies will be discussed in detail in Chapter 8. Here, we refer to the work of J R Spreiter (1950) and of W C Pitts et al. (1957) on slender-wing-body combinations and to other methods which have already been mentioned.

For slender wing-body combinations, the lift acting on that part of a configu­ration upstream of a given transverse plane depends only on the shape and size of the section of the configuration cut by that plane and on the streamwise rate of change of the section. The size of the body can be described by the parameter A* = jF/s^ , where F is the cross-sectional area. The effects which volume asymmetrically disposed may have on the lift are summarised in Fig. 6.70, from results obtained by R S Bartlett (1964) for circular cylinders carrying wings at different vertical positions, by H Portnoy (1968) for semi­circular bodies mounted beneath wings, and by R D Andrews (1968) for fuselages with rectangular cross-sections. In all cases, the bottom surface of the

LIVE GRAPH

Click here to view

Fig. 6.70 Lift generated by wings and bodies

fuselage is assumed to be parallel to the wing and the side-surfaces are assumed to lie along the freestream direction, i. e. the fuselage does not produce either streamwise compressions or expansions by itself in the trans­verse plane considered. The calculated lift L is expressed in terms of the lift

L0 “ 2raIIpV0!t

carried by a thin slender wing of the same span at the same angle of incidence, which is the linear lift term in (6.38). We find that wingless ellipses always give L = Lq, whereas wingless rectangles produce a lift which increases monotonically with A* . On all the other configurations, with wings, the interference is unfavourable at first, as A* increases, and L/Lo reaches a minimum. L/Lq then increases again as A* increases further. The calcualted lift gains above that of the wing alone can be substantial, but the results in Fig. 6.70 may only give an indication of the general trends: it is not clear how the flows implied in the theory can be realised physically.

Lastly, we mention briefly a special problem which may arise in the design of ogee wings with pronounced changes of the local angle of sweep along the lead­ing edge, where the leading edge may be nominally subsonic along some parts and nominally supersonic in others. Such shapes may have some attraction

because they have low values of the planform shape parameter p, which could lead to low drag values according to (4.140). Possible types of flow around swept leading edges which are nominally near-sonic have been described by A Stanbrook & L C Squire (1964) and have also been investigated by E Y C Sun (1964). The singularities which linear theory predicts for wings with mixed subsonic-supersonic leading edges have been cleared up by J H В Smith et al. (1968). However, there is no evidence that such wings have real advantages over wings which are aerodynamically slender and have the simple stable type of flow associated with them.

6.9 Some problems of complete aircraft. Since slender aircraft as considered here are basically constant-geometry wings, many of the problems concerning the complete aircraft have already been discussed above in the context of wings alone. In particular, some of the work on problems of stability and control at low speeds has been mentioned in section 6.5. Here, we want to follow this up by a brief discussion of some further problems concerned with flight dynamics; propulsion and engine installation; and sonic bangs.

In the field of flight dynamics and handling characteristics, we note that the design concept of slender wings implies that some problems which are prominent in the design of classical and swept aircraft simply do not arise: problems associated with variable-geometry devices or with interference effects between the wing, the fuselage, and the tailplane assembly do not appear in the design of constant-geometry slender-wing layouts. On the other hand, we must be aware from the beginning that we are in the middle of a development which may bring about radical changes: from the classical approach of designing for the dichotomy of stability and control to the introduction of active control as an integral part of aircraft design. These matters have been set out clearly in a review by W J G Pinsker (1974) of the scope of active control in the design and operation of aircraft. When we discuss below the more conventional approach to these problems, we should bear in mind that future developments may bring about new and improved design methods for automatic control, stabil­ity and control augmentation, artificial static stability, gust and flutter alleviation, and various methods for reducing wing loads. The application of these methods may alter many design and operating traditions and affect not only the aerodynamic but also the structural design and bring with them considerable benefits. For example, Pinsker has estimated that, by placing the centre of gravity behind the aerodynamic centre of a typical slender transport aircraft, the lift available for take-off and landing at a given angle of incidence could be increased by as much as 20%, and the drag reduced.

There is an important role of theory and calculations in studies of flight dynamics and in the refinement of flying qualities, as explained by H H В M Thomas & A J Ross (1972) and W J G Pinsker (1972). But much of the information needed has to be obtained from experiments, especially from flight tests, when transient responses in manoeuvering flight are involved. The problem of identifying the relevant aerodynamic parameters from the results of flight tests has been discussed by V Klein (1973) and A J Ross (1974). This supplements the work of A F Waterfall (1970) and of С H Wolowicz (1972) already mentioned in section 5.10.

Consider now some specific problems which are typical of large slender air­craft. On the airfield, there is the problem of rotation at lift-off and its implication for tail clearance requirements. The dynamics of this motion have been clarified by W J G Pinsker (1967). Piloted simulator studies by В N Tomlinson & T Wilcock (1967) revealed no serious problems and demonstrated the usefulness of a take-off director device. Two conditions on the approach to land, which might be expected to pose some problems are: flight in strong crosswinds and associated turbulence and the sidestep manoeuvre which may be required to align an aircraft with the runway when it breaks cloud and finds itself displaced laterally from the runway. The response of slender aircraft to sidegusts and means for its suppression have been worked out theoretically by В Etkin (1959) and by W J G Pinsker (1961). The theoretical results have been confirmed and supplemented by simulator studies and by flight tests with the HP 115 and ВАС 221 research aircraft, see A McPherson (1968) and F W Dee et al. (1968). The problems have been reviewed in the context of automatic landing by M J Lighthill (1962). Pilots have not reported any particular difficulties. Landings have been made with the ВАС 221 aircraft in cross­winds up to 12 knots, with a total wind of 20 knots, using the crabbing tech­nique, where the aircraft retains a moderate angle of yaw, or drift, during landing. Considerable control activity was required throughout the range of test conditions. Because of the aircraft’s relatively high approach speed, the highest drift angle at touchdown was only 4|° and the pilots either removed the drift by gentle rudder application, or landed without correcting the drift. Sidestep manoeuvres were made from an initial displacement of over 100m from the centre line of the runway, starting at an altitude of about 100m, in crosswinds up to 10 knots. Pilots found the coordinated S-turn easy to perform, despite the oscillatory roll response to aileron inputs. The largest bank angle used was 30°, and the time required to complete a sidestep manoeuvre was comfortably between 10 and 15 seconds. We have already mentioned in section 6.5 the favourable effect of ground proximity in these manoeuvres.

Thus slender wings are inherently easy and safe at take-off and landing.

There is again the problem of the vortex wake and its effect on following air­craft, which has already been discussed in section 5.7. There is evidence that the vortex cores behind slender wings decay and disappear much sooner than those behind classical aircraft (see e. g. R L Maltby & F W Dee (1971) and G H Lee (1973)), so that the vortex wake of an aircraft like Concorde presents less of a hazard than that of a classical aircraft of similar size.

Another special problem is the behaviour of slender wings on entering and leaving vertical upgusts and in flight in continuous turbulence. Experimental measurements of the transient pressures on a slender wing in a vertical gust, obtained in a specially designed facility, have been reported by G К Hunt et al. (1961) and by D R Roberts & G К Hunt (1966). A remarkable result of these tests was that the extra lift due to an upgust takes some time to build up, whereas it vanishes much more quickly when the wing returns to undisturbed air. This behaviour has not yet been fully explained, but several theoretical models of gust penetration have been discussed by G W Foster (1974). When working out the gust response, it is necessary to take account of the flex­ibility of the aircraft. Theoretical studies of dynamic aeroelastic effects on stability, control, and gust response have been carried out by E Huntley (1961), J К Zbrozek (1963), W J G Pinsker (1963), C G В Mitchell (1967) and

(1970) , and E G Broadbent et al. (1972). Further experimental work has been described by J M Simmons & M F Platzer (1971) and by J H Horlock (1974).

Another phenomenon which is peculiar to slender aircraft is flight at or near the zero-rate-of-climb speed (Vzrc) which is defined as the minimum speed, under a given set of conditions, at which an aircraft can maintain level flight. Such a condition obviously exists for all types of aircraft, but it has no operational significance on classical and swept aircraft which stall.

On slender aircraft, however, with no stall and with a large increase of lift-dependent drag at low speeds, flight at low altitude near this condition can be potentially hazardous (although much less dangerous than a conventional stall), since the pilot may not be aware of approaching or passing the zero – rate-of-climb speed because adverse aerodynamic handling features, which normally precede the stall and warn the pilot, are absent in this case. Furthermore, as the zero-rate-of-climb condition is not purely aerodynamic in origin, it is not associated with a particular equivalent airspeed, as is the conventional stall, but the zero-rate-of-climb speed varies with altitude, power setting, aircraft weight, air temperature, and aircraft configuration. There are three main problems of practical importance: the likelihood of the airspeed falling below VZrc ; the accuracy of determining the value of Vzrc; and the consequences of a speed reduction below VZrc in terns of the height losses incurred during the recovery to a speed safely above Vzrc • These problems have been clarified and solved for practical purposes by theoretical work of W J G Pinsker (1966), by flight tests by C S Barnes & 0 P Nicholas

(1967) , and by simulator studies by T Wilcock (1970). The experimental results agreed very closely with the theoretical predictions. It turns out that the energy associated with the height loss is used partly to increase the speed of the aircraft and partly to overcome the excess of drag over thrust when flying below Vzrc • As would be expected, the first effect is generally by far the larger but, in some manoeuvres, the drag term accounted for up to 30% of the total height loss. It also appeared that the best recovery technique is the most rapid one possible, to be effected by a positive manoeuvre involving a brief but rapid loss of height during gain of speed.

In this context, we mention a related problem which is not confined to slender wings only, namely, that of the glidepath stability of aircraft flown under speed constraint. There is a tendency towards a speed instability when an aircraft is flying in the approach on the backside of the drag curve. This may be corrected by the use of an autothrottle: the system can provide an absolute speed hold, i. e. the airspeed can be maintained even in the event of substantial changes in flightpath angle. Thus the modern autothrottle allows the pilot to select the desired approach speed and thereafter to virtually forget airspeed as a parameter to be monitored further. However, this system inhibits the fundamental energy-exchange mechanism between speed and height which normally stabilises the glidepath (see e. g. J G Jones (1971)), so that the aircraft can rapidly change its flightpath by a substantial amount without the normal self-corrective action coming into play and without the speed changes which might otherwise have alerted the pilot. This phenomenon has been clarified by W J G Pinsker (1971) who suggested that, when autothrottles are to be used in otherwise manually-controlled approaches, the speed lock should be removed or at least weakened.

Yet another instability which may be encountered by slender aircraft at very high angles of incidence is a form of sideslip divergence, i. e. a tendency to diverge to higher angles of yaw, when all lateral modes of motion of the air­craft, including the Dutch roll (see section 6.5), remain stable. In flight tests at very high incidence with the ВАС 221 research aircraft, it was observed that pilots applied tight aileron control so as to maintain level bank angle. Assuming such a bank-angle constraint, W J G Pinsker (1967) then developed a theory which suggested that the condition could be alleviated by reducing the adverse yawing moment due to aileron deflection. This was realised on the aircraft by an appropriate interconnect between the ailerons and the rudder. Subsequent flight tests confirmed the efficacy of this technique.

No serious stability or handling problems are known to arise during the super­sonic phase of the flight of slender aircraft, although there is an influence of the variation of engine thrust with speed and height on the dynamic stab­ility of the longitudinal motion. This has been discussed by G Sachs (1972). There have been fears that a slender aircraft might respond excessively to an engine failure at supersonic speeds, but these have now been completely allayed by a great deal of research work and information from flight tests, which has been summarised by C S Leyman & R L Scotland (1972).

This brings us to a brief discussion of some problems of propulsion and of engine installation. Means for generating propulsive forces have already been discussed in Chapter 3 and, considering the various types of engine available, we may conclude that a straight turbojet engine is very suitable for flight at a Mach number of 2 or just above that. As discussed in section 6.2, such an engine should also provide the thrust needed for take-off. Future develop­ments may go beyond this and use engines with more complex and efficient cycles, such as a variable-cycle engine in which the airflow is temporarily increased at take-off, to reduce engine noise, without increasing the frontal area of the engine.

It now remains to decide how such an engine should be installed. Some of the design methods discussed in section 5.9 still apply but, in the case of slender wings where the means of providing volume and lift can already be integrated, it is possible, in principle, also to integrate the means of propulsion with them. In an ideal and simple case of turbo-jets of equal intake and exit area, where the intake is running full and the jet is fully expanded at the nozzle exit, the engines need not be installed in isolated nacelles. Instead, they may be installed on the upper or the lower wing sur­face in such a way that a streamtube of the wing flow is used in part as the external surface of the powerplant, with the bulk of the engine buried inside the wing. This is quite possible in principle with a thick lifting wing like wing C discussed above. If the powerplant is small enough, the external pressures and forces on the combination are the same as those on the wing alone, to a first order, and the internal forces on the installed engine are the same as on the engine in isolation. This implies that the wing can be designed without taking account of the engine, and that the engine may be installed without any additional external drag, in contrast to podded instal­lations on swept wings, say, where the installed drag of an engine may be twice, or more, the drag of the isolated engine nacelle alone. As we shall see, we are far from achieving this ideal state in practice and we depart from it in many ways, for various reasons, but the potential benefits should always remain as an aim before us (see e. g. L F Nicholson (1957)).

In principle, again, the ideal installation of engines would be near the centre line on the top surface of slender wings in the region of parallel flow between the attachment lines, as indicated in Fig. 6.19. This should avoid the poss­ible ingestion of debris which may occur with the engines installed on the lower surface; it should provide a strong backbone and lighten the structure weight; and it should provide noise shielding, as discussed in section 5.9.

We have yet to learn how to exploit these potential benefits.

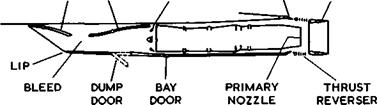
A real engine nacelle, as installed on the Concorde and described by C S Leyman & D P Morriss (1971) is shown schematically in Fig. 6.71. Later minor modifi­cations, to give more performance, have been described by M Wilson (1974).

This nacelle is installed on the lower surface; it is very much larger than the actual ‘gas generator’: compressor, combustion chamber, and turbine.

RAMPS SHUT-OFF NOZZLE NOZZLE FRONT REAR FLAPS DOORS SHROUD Fig. 6.71 Schematic layout of a supersonic powerplant. After Leyman Morriss (1971)

Intake and nozzle take up a great deal of the length of the nacelle. Another supersonic engine installation has been described by W C Swan (1974). General design principles have already been discussed in sections 3.7 and 5.9 (see also AGARD Conference Proceedings CP 91, 1971).

The supersonic compression in the intake may be partly external and partly internal, followed by a subsonic diffuser. The geometry of the intake can be varied by moving ramps. They are fully open up to about Mg = 1.3 . Above this, the ramps are progressively moved so as to reduce the throat area of the intake and to maintain the final intake shockwave on the intake lip.

E L Goldsmith (1966) has shown that the need for variable-geometry intakes arises in two ways: from the need to match engine and intake mass flows under all flight conditions, and from the need to maintain a high pressure recovery in the intake together with a low external drag over a range of Mach numbers. To avoid separation of the boundary layer from the walls, a large bleed hole is incorporated as well as doors and other openings, leading to a secondary airflow duct. Some drag is, of course, associated with such boundary-layer bleeds, see e. g. E L Goldsmith (1966). The nozzle is also of variable geo­metry and incorporates the secondary airstream. If the nacelles are grouped in pairs, a serious base-drag problem may arise. For experimental data on such layouts, we refer to tests by J W Britton (1965) and M D Dobson (1966). Nacelles installed in this way do interfere with the wing flow and are them­selves affected by it. These interference problems have been investigated e. g. by M D Dobson (1968) and J Leynaert (1974).

Next, we refer briefly to some work on tne problem of the so-called sonic bang op boom. This is the rather spectacular phenomenon which causes the pressure on the ground to change audibly, roughly in the form of an N-wave, when the system of shockwaves and expansions generated by an aircraft in supersonic flight reaches the ground. We are then interested in the farfield of the dis­turbances. The phenomenon itself has been known for a long time from the flight of projectiles, and theoretical work on the problem goes back to L Prandtl (1938). The theory of G В Whitham (1952) and (1956) and F Walkden

(1958) is concerned with farfield effects of weak supersonic disturbances and forms the basis of most of the current theories of the sonic bang. According to this theory, which is related to the supersonic area rule, the farfield effects, in a given direction, of a body or of a lifting wing are the same as those of an equivalent body of revolution. This amounts to replacing the disturbances by some equivalent cylindrical waves. There is now an extensive literature on the subject, and we refer here to reviews by С H E Warren &

D G Randall (1961) and by A R Seebass (1967), and to a practical numerical method by W D Hayes et al. (1969). Effects of density stratification, tempe­rature gradients, and turbulence in the atmosphere can now also be taken into account, see e. g. R Stuff (1970) and J A Beasley (1974), and predictions of the pressures have been made to an accuracy of about ±5%, compared with results from actual flights. Research work continues in order to take account of higher-order effects and to generalise Whitham’s approach, e. g. by M Landahl et al. (1973) and by К Oswatitsch (1972), the latter using an analytical method of characteristics. The accuracy of this method has been questioned by A R Seebass & A R George (1974), and this matter has not yet been fully resolved.

Attempts have also been made to find lower bounds to the bang or to minimise the peak overpressure or impulse, or to maximise the rise-time, see e. g.

L В Jones (1961), (1967) and (1970) and also A R Seebass & A R George (1974).

It turns out to be difficult to improve one aspect by much without adversely affecting the others, but any improvements in the general efficiency of the aircraft will tend to reduce the sonic bang also. Specifically, increases in the lift-to-drag ratio or thrust-to-weight ratio, or decreases in specific fuel consumption or overall weight, will all decrease both the overpressure and the impulse. However, the instinctive remedy of increasing the altitude of flight may actually increase the impulse due to lift. Moreover, it is at moderate altitudes that there is a chance of utilising any favourable effects that occur in the midfield, before the bang signature attains its final N-wave form.

Our knowledge of the effects that sonic bangs may have on people and on build­ings is still rather incomplete and uncertain. It seems to emerge that the effects on people are psychological rather than physical, and thus very difficult to assess. Many tests have been made on the effects of bangs on various structures, such as window glass in a building (see e. g. G W Zumwalt

(1966) ) or bridges (see e. g. V X Kunukkasseril & R Ramakrishnan (1974)). Historic buildings, particularly churches, were at one time thought to be in special danger of damage by bangs, but it seems clear now that the bang noise is generally less than that caused by such natural hazards as bells and organs. Many of these tests have been made by bang simulators (see e. g. J J Gottlieb

(1974) ), and we mention here the portable simulator for field use developed by N D Ellis et al. (1974). These devices have been applied, for example, to test the lifetime of plaster panels; a study which led to the conclusion that plaster in good repair is unlikely to be significantly damaged by repeated exposure to sonic booms generated by overflights of supersonic transport air­craft (see В R Leigh (1974)). In another study by 0 V Nowakiwsky (1974), the effects of simulated booms on the behaviour of car drivers were examined statistically, leading to the conclusion that current commercial supersonic aircraft under normal flight conditions will not produce adverse effects on a driver’s stopping distance or his ability to follow a particular course. We may mention in this context that supersonic transport aircraft are not expected to have any other harmful effects on the environment; they will cause climatic effects far less than those minimally detectable.

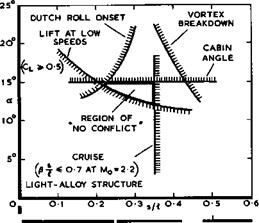
Finally, it may be useful to summarise in one simple illustration some of the limitations which arise in the design of slender aircraft from various stabi­lity and performance aspects and to demonstrate that there is a region where these are not in conflict. Several of the aspects which have been discussed impose limits on the geometry of slender shapes suitable for supersonic trans­port aircraft. How all these fit together is shown in Fig. 6.72, which

LIVE GRAPH

Click here to view

I J.. О I 2 A FOR DELTA WINGS Fig. 6.72 Various typical design limitations

summarises in a general way the essential limitations for typical conditions. The geometry of the aeroplane is simply represented by the shape of the box, s/£ , into which it fits. A number of the limitations are concerned with the low-speed behaviour. A line on the left-hand side gives an indication of the region which would be dominated by the onset of the Dutch-roll motion. This could now be defined in more detail as a result of the theoretical work men­tioned above, but we find that it does not present a serious practical limita­tion. On the right-hand side, a line is drawn beyond which vortex breakdown and significant pressure fluctuations on the wing surface may be expected.

The line is drawn for an angle of sideslip of 5°, which corresponds roughly to a crosswind of 15 knots in the approach. A third line, drawn at a = 15° , is meant to indicate that the cabin floor angle cannot be allowed to exceed certain values during take-off and approach, mainly for reasons of comfort.

The precise limiting number depends on the particular layout; and other criteria such as undercarriage length may be more practical, but some limit of this type always occurs. A fourth consideration is the lift coefficient which must be available in the approach to ensure safe landing speeds. At best, Cl – 0.5 for a long-range aircraft is a suitable criterion. These four low-speed limitations leave a region within which the proportions of an aircraft could be chosen. But on the right-hand side, the region will be bounded by considerations of cruise performance and here, for simplicity, a very complex aspect has been reduced to one line, defined by the assumption that the box into which the aircraft fits is aerodynamically slender at Mach numbers for which light-alloy structures are usable. All these limitations taken together leave a region within which the various requirements can be met and are not in conflict: no special measures are needed in order to meet the various conditions. This compatibility of the design aspects confirms that slender wings do indeed constitute a useful major type of aircraft.

All the matters dealt with in this chapter refer to A New Shape in the Sky (see M В Morgan (1972), R D Fitzsimmons (1974), R Chevalier (1974)). Concorde and its Russian counterpart the TU 144, represent the first generation of this new type of slender aircraft. They will have to prove their worth.