Numerical Solution of the Blasius Equation by Finite Differences

Because computational methods are emphasized throughout this textbook, we now describe an alternate numerical approach to the flat-plate boundary-layer solution that introduces CFD methods. Of course, we cannot undertake an in-depth dis­cussion of all of the subtleties of these methods. However, the present problem rep­resents an excellent opportunity to introduce a powerful procedure for obtaining solutions to otherwise intractable boundary-value problems.

We introduce the subject with no pretense of completeness and let the interested student seek further. Here, we primarily are interested in applying an approximate solution procedure to a nonlinear, ordinary differential equation and using these results in our boundary-layer analysis. Thus, the subject is developed as it applies to the Blasius equation given by:
with boundary conditions:

m=f ‘(о)=o, r o-)=1

as before. For simplicity we introduce:
g = f’
so that the Blasius equation becomes:
О II bo ‘4-І + * bo <N	(8.56)
with boundary conditions given as:
f (0) = g(0) = 0, g(-) = 1.	(8.57)

In what follows, we attempt to represent the derivatives by their finite-difference equivalents. Only the derivative normal to the surface must be accounted for in this simple problem. In effect, the integration in the direction of the flat plate already was accomplished. That is, we are dealing only with an ordinary differential equation rather than the partial-differential equation that must be confronted in a more general problem. The point to remember is that the same approach could be applied in the case of more independent variables, which we do in later applications.

Note that Eq. 8.56 is linear in g. However, it is still a nonlinear equation and we set up an iterative solution procedure at selected points in the domain. Here, the domain is the boundary layer. Thus, we divide the domain into a set of discrete points and number them from 1 to N (with N being the number of points that we are using). We choose to place the first point on the wall and the last point at the edge of the boundary layer. The next step is to create an approximate solution method whereby we find the values of the variables at these points. We do so by using these values and Taylor-series expansions to replace the derivatives in the equation with finite differences.

We note from the general Taylor series for a function f(x) evaluated at a nearby point, x + Ax, that:

Ax2 At3 Ax4

f (x±Ax) = f'(x) + f'(x)Ax + f "(x)^2- ± f’"(x^3L + f ""(*) ± … (8.58)

Thus, in terms of our independent variable, n, we have:

f (n ± Ат|) = f ‘От) ± f"(4+Ато+f At ± f"’ От) +f "00 Af ± … (8.59)

Now, with An being the spacing between points in the domain, we can see that:

if	fi = f(n),
then	fi+1 = f(n + An),	(8.60)
and	i p" и

By adding or subtracting Eqs. 8.58 and 8.59, it is now possible to find the expressions:

f ‘(^=fi+12An-1 -1r’ w Af+0( ^3)

(8.62)

We note that the second and remaining terms on the right-hand side of Eqs. 8.61 and 8.62 are of much smaller size (small An and derivatives not too large) than the first and we choose to drop them. This gives an algebraic expression for the first and second derivatives.

Next, we apply Eqs. 8.61 and 8.62 to Eq. 8.56 for g(h). This results in:

gj+1 – 2gi + gi-1 + f gi+1~ gi-1 = 0 An2 f 2 An!

which is a second-order approximation to Eq. 8.56. Eq. 8.63 can be rewritten by collecting the coefficients of the different g’s to obtain:

or Cigi=1 + bigi + agi+1 = 0, (8.64)

where:

The subscript i now refers to the fact that Eq. 8.64 represents the equation arising from applying finite differencing to the Blasius equation at the ith grid point. Also notice that the coefficients are functions of f and, hence, vary throughout the domain.

We note that Eq. 8.64 is applicable to every point in the domain from i = 2 to i = N-1 (we already know the values at i = 1 and i = N; these are the boundary con­ditions). Thus, there are N-2 equations for the N-2 unknown values of g. (We address the unknown value of f after setting up a procedure for g.) Applying Eq. 8.64 at each point between i = 2 and i = N-1 yields a linear system of the following form:

. (8.65)

This shows how to calculate the N-2 values of g. We would be finished were it not for the fact that we have not yet found the fj’s. To do this, we recall that f and g are related through Eq. 8.57 and we can find the values of f once we have found gi by a simple numerical quadrature. However, we still need values for f to obtain the values of g from Eq. 8.65. Thus, we make an initial guess for the g’s and compute the fs from this guess. Once we have found new values of g, we then can recompute f. This iterative process repeats until the solution no longer changes.

When the solution no longer changes, we say that the process has converged. Generally, the way this is checked is to see whether the maximum change in one variable is no larger than a small number. We call this number the convergence cri­terion. In our process, we check for the maximum change in g to be no larger than some reasonably small number—say, |Agi |max < 10-6.

We now return to obtaining the values of /. Recall that f = g; hence:

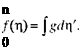(8.66)

Because we only know g at discrete points, we must approximate this integral. We do this using the trapezoidal rule. Thus, Eq. 8.66 becomes:

і 1

fi = X 2(gj + gj-iX^j – Vi)- (8.67)

j = 2 2

The summation starts at 2, recalling that f is at the wall and has a value of zero. Now, we can set up the entire numerical procedure as follows:

1. Select N and the height of the domain (maximum value of h).

2. Make an initial guess for the value of g at the points in the domain (linear between the boundary values suffices).

3. Find values of / in the domain from Eq. 8.67.

4. Solve Eq. 8.65 for new values of gi in the domain.

5. Check whether the process converged.

6. If not converged, repeat from Step 3.

7.

When converged, both g and/now are known at all points in the domain and the boundary-layer properties may be computed from them.

8.7 Results from the Solution of the Blasius Equation

Certain parameters describing the laminar boundary layer on a flat plate (i. e., zero pressure gradient) may be evaluated using the solution of the Blasius equation. The definitions of the parameters are valid for either a laminar or a turbulent boundary layer, with or without a pressure gradient. After the key parameters are defined, their values are expressed for a laminar boundary layer (i. e., Blasius profile) on a flat plate. Although the freestream flow is little disturbed by the
presence of the flat plate, the velocity at the outer edge of the boundary layer is denoted by Ue(x) rather than a constant value such as Vж implied in the flat-plate solution. This allows for later generalization. In particular, the former notation implies that the velocity outside the boundary layer is allowed to change in the x-direction as required by an imposed pressure gradient or as a result of curvature of the surface.