POWER REQUIRED IN A VERTICAL CLIMB

The power required in a vertical climb is higher than that required in hover primarily because of the change in potential energy. Secondary effects are the increased vertical drag, increased tail rotor power, and decreased induced power since the rotor is handling more air. For simple calculations, the profile power of the main and tail rotors can be considered to be the same in climb as in hover.

For this analysis, the equation for vertical drag will be written:

^(vlc*VcyAM + (AAzCD) Vc

Dy G. W.

Dv= 4

where AAz is the area of the portion of the airframe not in the wake and CD is the drag coefficient of the additional area.

From the momentum equation:

The tad rotor thrust required to balance main rotor torque is:

Pm Pm

(Щм It

and the tail rotor power is:

R,

(Щм It.

For this analysis, it will be assumed that the tail rotor-induced velocity remains a constant at its hover value and that the tad rotor power is directly proportional to tail rotor thrust alone. The rationale for this assumption is that even though the thrust of the tail rotor increases in climb, it goes into a forward – flight condition where it handles more air and thus produces less induced velocity for the same thrust. The total power is:

and the difference in power between climb and hover is:

An opportunity to check the validity of this equation is provided by the flight test data of reference 2.1 for an AH-lG. Figure 2.3 shows the correlation and also the difficulty in obtaining this type of test data. For example, at a power increment of 150 h. p., the measured rate of climb varied from 570 to 1,180 ft/min.

Source: Ferrell & Frederickson, “Flight Evaluation Compliance Test Techniques for Army Hot Day Hover Criteria," USAASTA Project 68-55, 1974.

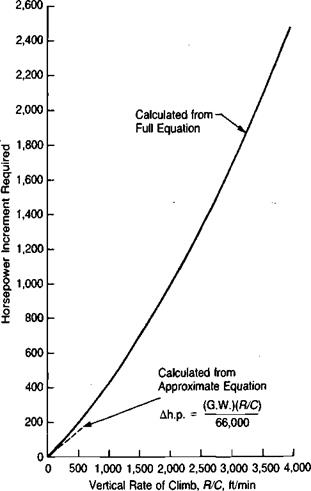
Figure 2.4 presents the results of the same type of analysis for the example helicopter.

A simple method for making a quick estimate of the incremental power for low rates of climb can be obtained by ignoring the vertical drag and tail rotor effects in the above equation. Then:

. G. W. ,

Ah-P – = ^-(4 + Fc-40I)

or

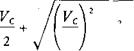Ah. p. =

FIGURE 2.4 Power Required in Vertical Climb, Example Heli­copter

It may be seen that for low rates of climb such that

the change in power is simply:

G. W. Vc 550 T

which is just half of the value which would be computed based on the rate of change of potential energy. For the example helicopter at a vertical rate of climb of 500 ft/min—or 8.33 ft/sec—the two velocity terms are:

and

fa J2 = (39)2 = 1,521

Thus the criterion can be considered to be satisfied for this case. The first approximation to the extra power required to climb at this rate for the example helicopter is 150 h. p., as shown in Figure 2.4. A more detailed analysis of vertical climb is given in reference 2.2.