Prandtl Lifting Line Theory
15.5.2.1 Origin of Induced Drag
The remarkable feature, in the flow past a finite wing, is the existence of a vortex sheet, originating at the sharp trailing edge and trailing the wing to downstream infinity (Trefftz plane ST). In the proximity of the vortex sheet, which is made of vortex filaments parallel to the incoming flow, the flow field is perturbed. Far downstream, in the Trefftz plane, the pressure returns to the undisturbed static pressure, hence uT = 0 (since Cp = —2u/U). However, vT, wT = 0. An energy balance, applied to a large control volume, Fig. 15.17, shows that the energy in the Trefftz plane is larger that the incoming flow energy. Therefore, some positive work has been done to the fluid. This work is that of a thrust force which balances an equal and opposite drag force (induced drag). It can be shown that
![]()
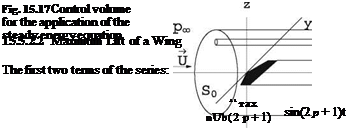 |
 |
See the corresponding distribution of circulation and downwash, Fig. 15.18. There is no upwash, as one finds wT(y) = —8UA Ц – < 0.
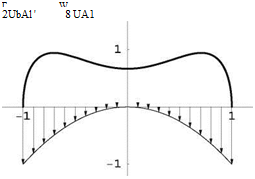 |
Fig. 15.18 Circulation and downwash
15.5.2.3 Induced Drag
The induced drag can be written
showing a 33 % loss compared to the elliptic loading.
The induced drag due to two finite strength vortices is obtained when all the terms are added in the infinite series, i. e.
This is a diverging series.













