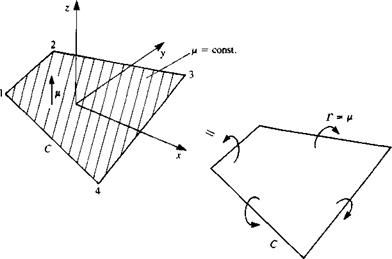
Quadrilateral Doublet

Consider the quadrilateral element shown in Fig. 10.15, with a constant doublet distribution. Using the doublet element which points in the z direction the velocity potential can be obtained by integrating the point elements:

zdS

[(x-x0 )2 + (y-y0)2 + z2f/2

This integral for the potential is the same integral as the w velocity component

FIGURE 10.15 Quadrilateral doublet element and its vortex ring equivalent.

of the quadrilateral source and consequently

Ф = – p – [tan" 4 ж L	tan-	^wi12e2 – h2^
+ tan-1	tan"1	(т2ъеъ – лз j
+ tan-1	ио_1(	(‘/П34Є4 – л4 ( zr4 /
+ tan-1	tan_,	{m^ei-hiY К zr! / J	(10.105)
			(10.106)

The velocity components can be obtained by differentiating the velocity potential

ЗФ ЭФ ЭФ

4л – [(x – *!)(* – x2) + (y – yO(y – y2) + z2]} z(y2-y3)(r2 + r3)

hr2{rxr2 – [(x – XjKx – x2) + (y – y,)(y – y2) + z2]} ________________ z(x3-x2)(r2 + r3)__________________ r2r3{r2r3 – [(x – x2)(x – x3) + (y – y2)(y – y3) + z2]} ________________ z{xA – x3)(r3 + r4)________________ r3r4{r3r4 – [(x – x3)(x – x4) + (y – y3)(y – y4) + Z2]} ________________ z(x 1 – X4)(r4 + Г])__________________ 1 – [(* – – ^i) + (у – y4)(y – Уі) + z2]} J [(^ – x2)(y – yQ – (x – xQ(y – y2)](rt + r2) ■гіГ2{ГГ2 – [(x – Xx)(x – x2) + (y – Ух)(у – y2) + z2]} [(x – x3)(y – y2) – (x – x2)(y – y3)](r2 + r3) r2r3{r2r3 – [(x – x2)(x – x3) + (y – y2)(y – Уз) + Z2}} [(x – x4)(y – Уз) – (x – x3)(y – y4)](r3 + r4) r3r4{r3r4 – [(x – x3)(x – x4) + (y – y3)(y – y4) + 22]} [(JC – *i)(;y – ^4) -(.X – x4)(y – уО](л4 + rj) 1

and following Hess and Smith101 they are
z(yi ~ y2)(ri + r2)
и =
(10.107)
z{x2 – Xi)(ri + r2)
+
+
(10.108)
+
	(10.109)
n [(x-x2)(y-y1)-(x-xl)(y-y2)](rl + r2) ц; =:————————————————————————– 4л L – [(x – Xi)(x – x2) + (у – Уі)(у – y2)]} | [(x – x3)(y – y2) – (x – x2)(y – y3)](r2 + r3) r2r3{r2r3 – [(x – x2)(x – x3) + (y – y2)(y – Уз)]} | [(x – x4)(y – Уз) – (x – x3)(y – y4)](r3 + r4) r3r4{r3r4 – [(x – x3)(x – x4) + (y – y3)(y – y4)]} 1 [(-у-^хХу-у^-^-^Су-УїЖ^ + ‘-і) 1 r4r1{r4r1 – [(x – x4)(x – Xj) + (y – y4)(y – Уі)]} j (Note that z = 0 must be used in the rk terms of Eq. (10.92), too.)

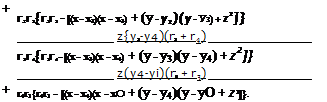In Section 10.2.2 it was shown that a two-dimensional constant-strength doublet element is equivalent to two equal (and opposite direction) point vortices at the edge of the element. Similarly, in the next section we will show that the three-dimensional constant-strength doublet element is equivalent to a constant-strength vortex ring that is placed at the panel edges. Therefore, the above formulas for the velocity potential and its derivatives are valid for twisted panels as well (but in this case when the point P lies on the element the u, v velocity components may not be zero).

FAR FIELD. The far-field formulas for a quadrilateral doublet with area A can be obtained by using the results of Section 3.5 and are

Ф(х, у, z) = z[(x – x0f + (y – y0f + z2]-3’2

_3M________ (x – x0)z________

“ 4* [{x-x0f + (y-y0)2 + z2r

ЗдА_______ (у-Уо)г________

4л [(x – x0)2 + (y – y0)2 + z2]512

M (x-x0)2 + (y-y0)2-2z2 4л [(x – x0)2 + (у – Уо)2 + z2]5f2

An algorithm for calculating the influence of this quadrilateral constant strength doublet panel is given in Appendix D, Program No. 11.