Quadrilateral Source

Consider a surface element with a constant-strength source distribution a per area bounded by four straight lines as described in Fig. 10.14. The element comer points are designated as (хг, yx, 0),… , (x4, y4, 0) and the potential at an arbitrary point P(x, y, z), due to this element is

<10s7)

and the velocity components can be obtained by differentiating the velocity potential:

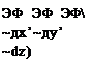
(10.88)

FIGURE 10.14 Quadrilateral constant-strength source element.

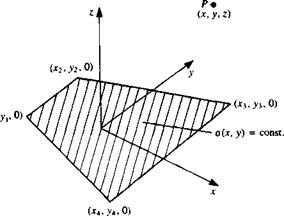
Execution of the integration within the area bounded by the four straight lines requires a lengthy process, and the results are obtained by Hess and Smith.101 Using their results, the potential for a planar element becomes

ф – <T f Г (x ~ *і)(Уі – Уі) ~ (У ~ Уі)(*г ~ *і) іп г + гг + <*іг 4я 1L dl2 r, + r2-d,2

| (* – х2)(Уз ~ >2) -(У – Уі)(х з ~ х2) 1п г2 + г3 + d23

^23 Ь + г3- d23

, (* – х3)(у4 – Уз) -(у – Уз)(*4 – *з) 1п Гг + п 4- </34

г/34 Г3 + г4 – d34

, (* – *4)(Уі – >4) -(у – У*)(хі – *4) 1п г4 + Гі + d4 л

d41 r4 + r1-dAl

+ tan

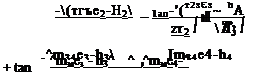du = V(*2 – *i)2 + (У2 – Уіf d-a = V(x3 ~ x2f + (л – Уг)2 dM = V(*4 – *з)2 + (У* ~ Уз)2 d*i = V(*i – x4f + (Уі – У*)2

Гк = л/(х – xk)2 + (у – yk)2 + z2 к = 1, 2, 3, 4 ek = (x – xkf + z2 к = 1, 2, 3, 4 hk = (x — xk)(y — yk) * = 1,2, 3,4 The velocity components, based on the results of Ref. 10.1, are

where

(10.90a) (10.906) (10.90c) (10.90d) (10.91a) (10.916) (10.91c) (Ю.9Ы) (10.92) (10.93) (10.94)

and

and

(10.95)

(10.96)

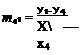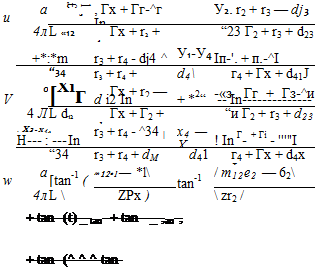The и and v components of the velocity are defined everywhere, but at the edges of the quadrilateral they become infinite. In practice, usually the influence of the element on itself is sought, then near the centroid these velocity components approach zero. The jump in the normal velocity com­ponent as z—»0 inside the quadrilateral is similar to the results of Section 4.4.

w(z = 0±) = ±| (10.98)

When the point of interest P lies outside of the quadrilateral then

w(z = 0±) = 0 (10.99)

-oA 4W(* – x0)2 + (y – y0f +

FAR FIELD. For improved computational efficiency, when the point of interest P is far from the center of the element (jc0, y0, 0) then the influence of the quadrilateral element with an area of A can be approximated by a point source. The term “far” is controlled by the programmer but usually if the distance is more than 3-5 average panel diameters then the simplified approximation is used. Following the formulation of Section 3.4 (in the panel frame of reference) the point source influence for the velocity potential is

The velocity components of this source element are

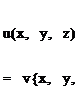________ oA(x – x0)________

4л[(х – x0)2 + (y – y0)2 + z2fa

________ oA(y-y0)_________

________ oA(z – z0)________ 4*[(*-x0)2 + (y-yo)2 + z2]3/2

4n[{x – x0)2 + (y – y0)2 + z2]3a

A student algorithm for calculating the influence of a quadrilateral constant strength source element is given in Appendix D, Program No. 11.