Results and Discussion

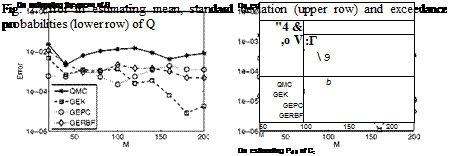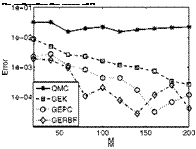
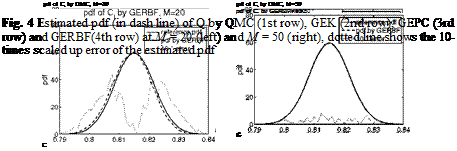
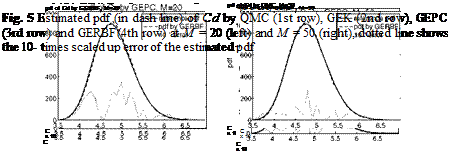
The results of the efficiency comparison are shown in Figure 2 to 5. Figure 2 and 3 show the errors of the four methods in estimating the target statistics of Q and Cd. It is observed there that the three gradient-employing surrogate methods, GEK, GEPC and GERBF are more efficient than the QMC method since the former three reduce their errors faster with an increasing cost measure M. Figure 4 and 5 depict the estimated pdf of Q and Cd obtained by the four methods, comparing with the refer­ence pdf. There we see that for the same computational cost, the surrogate methods yield much more accurate pdf’s. This is consistent with their relative performance in estimating the statistics.

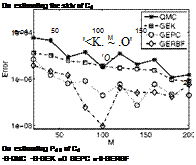Fig. 3 Error in estimating mean, standard deviation (upper row) and exceedance probabilities (lower row) of Cd

One of the reasons for the relatively better performance of the surrogate methods is that they utilize more information with the same computational cost M, i. e. they use (1 +сІ)Ц – conditions (SRQ samples and gradients) while a direct integration method like QMC uses M conditions (SRQ samples only). This advantage is due to the cheaper cost of obtaining gradients by an adjoint solver in the case that the number of SRQ’s is smaller than the number of variables d, and is expected to increase with an increasing number of variables, d.

Although it seems that GEK and GERBF perform better than the other surrogate methods in estimating statistics of Q and Cd respectively, it may not be appropriate to base a general conclusion on that. In Figure 4 and 5 we see the three surrogate methods have similar accuracy in their estimated pdf of Q and Cd.

The efficiency of GEK or GERBF is sensitive to the choice of the covariance model or the radial basis function and also to the value of the internal paramet­ers, and excelling configurations of them are problem – and data-dependent. In this work, different techniques are used for the optimization of the internal parameters, i. e., maximum likelihood optimization for GEK and leave-one-out error minimiz­ation for GERBF. This may also influence their relative efficiency, possibly differ­ently in the Ci and Cd cases. Due to the complex nature of comparative efficiency of

surrogate methods with different configurations and internal optimization tech­niques and different target SRQ, here we do not try to draw a conclusion on this issue.

In the estimation of the statistics of Q we see GEPC is not always reducing its error with an increasing M. This might be ascribed to the fact that the number of polynomial chaos (PC) terms is not truncated according to the order of PC, but to

an arbitrary number which is half of the number of available conditions. A set of PC terms that is “incomplete” for a particular order might not lead to more accurate ap­proximations than a set with less number of terms but “complete” for a lower order. Nevertheless, GEPC has a favored property that we have no burden of choosing the best-fitting configuration for it.

4 Summary

Gradient-employing surrogate methods have an advantage in handling aerodynamic uncertainty quantification (UQ) problems in the cases that an adjoint solver is used and the number of system response quantities (SRQ) is smaller than the number of variables so that the gradients of SRQ can be obtained at a reduced cost. These methods construct surrogates of the CFD model so that the statistics of an uncertain SRQ can be integrated on the surrogates models.

For investigating the efficiency of the different UQ methods we set up a test case where the geometry of an RAE2822 airfoil is perturbed by a Gaussian random field which is parameterized by 10 independent variables. Three surrogate meth­ods, gradient-enhanced radial basis functions, gradient-enhanced point-collocation polynomial chaos and gradient-enhanced Kriging, together with a direct integration method, quasi-Monte Carlo (QMC) quadrature, are applied to the test case and com­pared in their efficiency in estimating some statistics and probability distribution of the uncertain lift and drag coefficients. The results show that with the same com­putational effort the gradient-employing surrogate methods achieve better accuracy than the QMC does.