Slender Body Theory

Slender Body Theory is applicable to bodies such as slender fuselages and nacelles, and also to very slender delta wings with AR ^ 1. The key simplifying assumption, and the definition of “slender," is that the yz – plane cross sections of the body and the flow vary slowly in the streamwise x direction relative to the y, z directions. This implies that the streamwise component px of the perturbation velocity Vp is negligible compared to the transverse components py, pz.

Px < Py, Pz (6.59)

It’s useful to note the similarities with the Trefftz plane, introduced in Section 5.6.

6.6.1 Slender body geometry

The geometry of the body is specified by its surface position vector

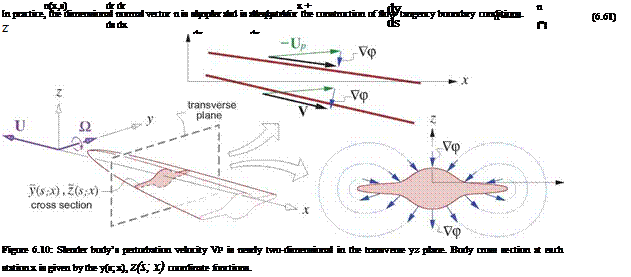where s is some parameter, such as the arc length in the yz plane. This defines the y, z cross-section shape of the body at some x location, as shown in Figure 6.10. Since the vectors dr/ds and dr/dx are both tangent to the body surface, the unit normal vector can be determined via their cross product.

6.6.2 Slender body flow-field

The body is assumed to move at steady velocity U = — V» X and pitch rate О = q y, so the local apparent freestream is —Up = — (U + О x r) = V» X + qxz. Any angle of attack or sideslip is assumed to be included in the r geometry definition. The perturbation potential p(x, y,z) of the flow about the slender body is assumed to locally satisfy the two-dimensional crossflow Laplace’s equation

Pyy + Pzz = 0 (for y2 + z2 < f2 ) (6.62)

where f is the length of the body. Dropping the pxx term has been justified by the slender-flow assump­tion (6.59). The appropriate boundary conditions are flow tangency of the total velocity on the body surface, and asymptotically zero perturbation flow far away.

[ (V»+Px) X + Py y + (qx + Pz)z ] ■ n = 0

or Py ny + Pz Uz ^ — (V» Ux + qx Uz) (onbody) (6.63)

and P ^ 0 (for y2+z2 » f2) (6.64)

The Pxnx term has been dropped from the right side of (6.63) since it is negligible relative to the other terms.

Laplace’s equation (6.62) and boundary conditions (6.63),(6.64) define a 2D incompressible potential flow with a known nonzero normal velocity —(V» nx + qxnz) which is due to the pitch rate and also the incli­nation of the body surface relative to the freestream x direction. Such a flow is sketched in Figure 6.10 on bottom right. It can be computed for a given arbitrary cross-section using any standard 2D panel method, but with a different righthand side than usual. To compute the overall 3D flow, some sufficiently large number of individual 2D problems would actually have to be solved, one for each discrete x location.

Poo + pV* -pVoo^Px – p (<Py + <pt)

Once the potential p(x, y,z) is computed, the pressure is determined using the Bernoulli equation.

Even though the streamwise perturbation velocity px was neglected in the local 2D problem defined by Laplace’s equation (6.62) and boundary condition (6.63), it is required for the pressure calculation. The reason is that VOpx is not necessarily negligible compared to +P2 and hence must be retained here.